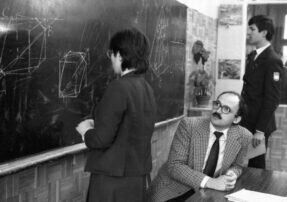Владимир Натанович Дубровский: 50 лет работы в Интернате

В сентябре 2019 года исполнилось 50 лет, как доцент кафедры математики Владимир Натанович Дубровский работает в нашей школе. Будучи сам выпускником интерната, он пришел сюда еще студентом мехмата преподавать математику и работал все это время, сначала в ФМШ №18 при МГУ, затем в СУНЦ МГУ. Множество учеников, разлетевшихся за эти полвека во все уголки земного шара, помнят его прекрасные лекции и семинары, вспоминают с благодарностью, как  терпеливо и внимательно он относился к каждому. Дверь в чудесный мир геометрии в частности и математики в целом для многих открыл именно он.

Поздравляем дорогого и уважаемого Владимира Натановича с этим прекрасным юбилеем и желаем еще многих лет преподавания в нашей школе!

Мы решили поговорить с Владимиром Натановичем обо всем, что происходило в эти годы.

Публикуем эксклюзивное интервью о годах работы в интернате и не только.

 

Учителя

— Давайте начнем с самого начала, вспомним время Вашей учебы в ФМШ 18. Наверное, Вам нравилось учиться в интернате, раз Вы пришли туда работать? 

— Конечно, нравилось. В преддверии нашего интервью я понял, что помню вообще всех своих интернатовских учителей.

— Как раз хотелось спросить, кто Вас учил?

— Я прямо по именам, по фамилиям помню, и не только по математике. Всех перечислять – все-таки это много. По математике, как у всех в то время, у нас было пять преподавателей, если не считать «элементарную математику».

— У Вас был двухгодичный поток (для тех, кто не знает)? Давайте обозначим годы обучения.

— Двухгодичный поток. 1965-67 годы.

— Получается, у Вас был 5-й выпуск?

— Это трудно посчитать в уме на самом деле. Первый выпуск был совсем маленький, а в какой-то год, кажется, в 66-м, было сразу два выпуска… Наш был то ли 4-й, то ли 5-й.

 — Кого-то можете назвать, кто более всего запомнился и сильней всего повлиял?

— Во-первых, по математике надо назвать Алексея Брониславовича Сосинского. Это у нас был не то чтобы кумир, не совсем то слово, но для всех, я думаю, один из любимых во многих отношениях преподавателей и лекторов. И потом он большую роль вообще в моей жизни сыграл в дальнейшем.

— Что он у вас вел?  

— Он читал у нас лекции по математике. Тогда лекции не делились по предметам. Было два часа лекций в неделю, но как они распределяются между предметами – это уже лектор определял.

— А откуда тогда бралось 5 преподавателей?

— А вот семинары уже делились по предметам. Грубо говоря, на «алгебру и анализ» и «геометрию», как-то так. У нас было даже не 5, а 6 преподавателей. Было две пары преподавателей, из которых одна пара вела анализ, это были Михаил Васильевич Козлов и Игорь Георгиевич Журбенко.

— Михаил Васильевич Козлов у нас тоже вел матанализ.

— А другая пара вела все остальное — это был Женя Гайдуков (Евгений Владимирович, но мы, кстати, преподавателей называли по именам, не по имени-отчеству, только для Сосинского было имя-отчество) и еще был один парень по фамилии Кузьмич, если не ошибаюсь, Костя. И Гайдуков же был нашей «классной дамой».

Точнее, у нас было три классных дамы. Сначала, в девятом классе,  была Антонина Дмитриевна, известная по прозвищу «Тигра» (но добрая), потом в десятом была Пирожкова Юлия Григорьевна – наверное, она и при вас была. Она потом довольно долго работала ночным воспитателем, уже в двухтысячных годах. И Гайдуков тоже был у нас. Я уже не помню, как это все комбинировалось, но, видимо, он выполнял функцию именно классной дамы. А настоящие «дамы» больше следили за чистотой и порядком, как-то так. В других классах были воспитательницы, как и сейчас. Но то ли был какой-то момент, когда они сменялись… В общем, у нас классным руководителем был Гайдуков. Это было необычно и интересно. А еще был у нас Игорь Константинович Сурин, шестой преподаватель математики. В интернате было два учителя, которые вели элементарную математику: один – знаменитый Шершевский, он был как-то более популярен – дольше работал, наверное, чем Сурин. А у нас был Сурин. Для нас он считался уже пожилым по сравнению с остальными нашими преподавателями.

— Остальные были аспирантами?

— Да, аспирантами-математиками. Кроме Сосинского, который тогда уже был доцентом. Сурина мы тоже любили, он вел у нас в десятом (выпускном) классе, 1 час в неделю. Это была фактически подготовка к вступительным экзаменам.

— У вас были КРКЗ?

— Вот это у него и было. Слово «КРКЗ» (Как Решать Конкурсные Задачи) вообще-то придумал Саша Земляков, позже. Но в смысле содержания этого предмета, я думаю, он следовал Сурину. То есть в принципе у нас это «КРКЗ» уже было. Тетрадочки у нас были, задания там по 20 – и это еще хорошо, если 20 – тригонометрических уравнений на неделю давались.

— Это был типа такой спецкурс?

— Нет, даже не спецкурс. Это в сетке был предмет. Он так и назывался – «Элементарная математика».

— У нас это было как дополнительное задание.

— У вас на самих занятиях было достаточно много этого КРКЗ, на той же геометрии мы много решали конкурсных задач, многие задачи ориентировались на экзамен, особенно по стереометрии.

— Очень помогло впоследствии при поступлении.

— А у нас тогда на этих предметах, которые аспиранты вели, вообще черт знает что проходили. Такое у меня осталось веселое впечатление.

— То есть у вас еще программы как таковой не было? Преподавали, что хотели?

— Нет, не что хотели. Были все-таки лекции.

— Насколько они соответствовали школьной программе на тот момент?

— Не очень соответствовали. Весьма относительно. Тогда Андрей Николаевич Колмогоров рулил лично, то есть все программы через него утрясались. Допустим, были лекции в 9-м классе о том, что такое действительное число, это начала анализа, и анализ занимал почти все время, большую часть лекций. Частично геометрия была. На геометрии были преобразования – движения, подобия, в 11 классе – абстрактная аффинная геометрия, еще помню площадь поверхности по Минковскому… Это то, что я помню.

— У вас Колмогоров читал лекции?

— Читал, но не в нашем потоке.

— А ЕЖи сразу образовались?

— Да, сразу. ЕЖи были тогда. Надо еще сказать, кто нам физику читал, потому что по физике лектором, и очень хорошим, был лично Исаак Константинович Кикоин. В 9-м классе он читал, в десятом уже продолжал Олег Николаевич Найда, тоже легендарный человек, который носил по разным ведомствам бумажки о создании интерната, он тогда совсем молодой был и ходил с этими бумагами по поручению Кикоина и кого-то еще, об этом написано в разных воспоминаниях. В классе у нас вел физику Грингауз, но не все время. Тоже известный человек, очень рано умерший, к сожалению.

— Когда проявилась Ваша склонность к математике? Уже в интернате? Был ли выбор между физикой и математикой?

— Нет, у меня такого вопроса не было. Это была, конечно, математика. Вообще-то у меня был выбор между математикой и лингвистикой, если уж так говорить.

Литературу в нашем классе вела Галина Николаевна Нагайцева. Здесь особенно вспоминать нечего. Галина Васильевна (Белоцкая) иногда приходила. А вот английский запомнился. У нас вела Галина Ивановна Ахманова. Вообще английским в интернате первые годы руководила, как сейчас бы мы сказали, была зав. кафедрой (хотя тогда такой должности не было), ставила иностранный язык Ольга Сергеевна Ахманова.

— Ольга Сергеевна Ахманова была зав. кафедрой английского языка у нас на физфаке.

— А у нас кафедры тогда не было, но она ставила преподавание языка. Галина Ивановна Ахманова была ее невестка, жена сына, она вела непосредственно у нас, была одной из любимых учительниц. Среди «англичан» в интернате в дальнейшем были замечательные люди, достаточно назвать Сашу Ливерганта, ныне главного редактора журнала «Иностранная литература». Но сказать, что сейчас у нас с английским все очень здорово, нельзя. Это проявляется, когда дети участвуют в разных международных мероприятиях. Например, в этом году мы участвовали в международном соревновании, где нужно было по-английски писать и рассказывать про математику, и детям это было трудно. Это надо поправлять у нас.

Нужно еще, конечно, назвать нашего директора Раису Аркадьевну Острую. Она тоже была выдающимся человеком, а у нас вела историю. Предмет прекрасно знала и рассказывала замечательно, можно было заслушаться. Историю Наполеона очень любила, много о нем рассказывала. Она заканчивала ИФЛИ, этот знаменитый институт, еще до войны. А во время войны она была на фронте и воевала в войсках связи.

 

— Она была самым первым директором?      

— Нет, она была вторым. Первым директором был П.А.Кузнецов, но я его уже не застал, он совсем недолго был, а потом Раиса Аркадьевна, и как раз при ней все так расцвело.

— А спецкурсы у вас были?

— Да, спецкурсы у нас были, и много. Более того, у нас считалось за доблесть посещать много спецкурсов – чем больше, тем ты более доблестный.

— Оценки за спецкурсы куда-нибудь шли?

— Нет, за спецкурсы не шли. Чемпионом по спецкурсам был Земляков. Он ходил на семь. Я ходил на шесть. У Сосинского, кстати, был очень интересный спецкурс, его я помню до сих пор – «рогатая сфера Александера» и прочее…

— Вы с Земляковым в одном классе учились?

— Мы не только учились в одном классе, мы с ним всю жизнь вместе, до окончания аспирантуры. Жили в одной комнате в интернате, в общежитии в университете, потом в одном блоке уже в аспирантуре.

— И пришли вместе в интернат работать?

— Он раньше пришел, еще будучи второкурсником. Я пришел после второго курса. Меня привел Валера (Валерий Федорович) Пахомов. Не то чтобы уговорил, там особенно уговаривать не надо было, а предложил. Он тогда год уже проработал. И мы работали втроём, у нас такая тройка была – Пахомов, я и Лукашенко Тарас Павлович.

— А что вы вели?

— А мы все вели. Я, честно говоря, не помню уже. И не помню, кто был во второй тройке в наших классах. Я помню, что когда я первый год работал, лекции по анализу читал Владимир Михайлович Алексеев, замечательный математик, примерно в то время получивший важный результат в задаче трех тел. Его тоже нужно вписать как одного из крупных математиков, которые у нас работали.

— Сложно ли было тогда поступить на мехмат после интерната?

— Наши вступительные экзамены – это был уникальный случай. Того человека, который сочинял этот экзамен, насколько я знаю, больше к составлению экзамена не подпускали. Обычно в варианте шесть задач, ну или пять. У нас было всего четыре задачи, пятерку ставили, если чисто решены три. По-моему, у нас пятерок было всего четыре штуки при поступлении, поэтому там золотые медали не сработали.

— Как Вы тогда себя чувствовали при поступлении в университет с интернатовской подготовкой? Уверенно?

— Уверенно, но задачи были такие… Там в одной задаче нужно было знать или вывести формулу площади сферического многоугольника. И вот ее почти никто не решил.

— Медали многие получали тогда в интернате?

— Вообще немногие. Но наш год, по-моему, был в этом смысле урожайным по сравнению с соседними, у нас 4 золотые медали было.

— У нас вообще не было ни одной.

— У нас было 4, вот как раз была у Землякова, у меня и еще у двоих: Володи Дербова из ЕЖей и Ильи Гарбера, он потом стал не математиком, а психологом.

— Получилось, что все равно Вы сдавали экзамены на общих основаниях?

— У нас было так: если сдаешь математику на 5, то все. Но там был такой экзамен, что черта с два его сдашь на 5.

Начало преподавания

— Получалось ли совмещать учебу на мехмате и работу в интернате?

— Да, мне давалась легко учеба, тем более, что я первые годы, пока был студентом, в основном все больше в подмастерьях работал у Пахомова. Постепенно он меня выталкивал к доске: иди, расскажи там что-то.

— А когда вы уже получили самостоятельность?

— Через несколько лет, точно не скажу. В любом случае, вначале, даже когда уже сам рассказываешь, все равно отвечает за все другой человек, ведущий преподаватель. Потом уже я лекции начал читать – в семьдесят пятом году. Я начал с геометрии, потому что кто-то там у нас закончил читать, может быть, Саша Абрамов. Раньше лекции по геометрии Колмогоров читал, но тогда была такая система лекций, что не было четкого их деления по предметам. Какой-то кусок в курсе математики отдавался на лекции по геометрии.

— Когда произошло разделение на предметы?

— Оно закрепилось, когда образовался СУНЦ. Это ввел Валерий Вавилов.

— Но у нас же уже были отдельно алгебра, анализ и геометрия. Это конец семидесятых – начало восьмидесятых.

— По факту было, но это еще могло варьироваться. Тогда лекционных часов было два, а не три.

— А Колмогоров ведь не только геометрию сам читал? Нам он прочел три первых лекции по алгебре.

— Он читал то, что считал нужным. Читал лекции и по анализу. В наше время он как раз свои учебники по анализу и по геометрии выпускал. По ним начали учиться в шестьдесят восьмом году.

— В интернате ими пользовались?

— Частично, они же на обычные школы рассчитаны. И вообще в интернате математику учили и учат не по учебникам. Но какие-то моменты он в интернате обкатывал. Интернат был своего рода полигоном.

—  Зачем вообще были нужны такие школы, как интернат?

— Разговоры об этом были с самого начала, когда только создавали интернат и когда его уже открыли. Я вспоминаю наши первые дни рождения, самый первый был как раз в шестьдесят пятом году, потом декабрьские собрания стали традиционными. Какие-то вещи запечатлеваются: я помню, как Ольга Сергеевна Ахманова выступала на одном из этих вечеров, прямо вижу, как она выступает. Яркое впечатление – автор толстенного словаря.

— В каком году это было?

— В 65-м или в 66-м. И на эту тему – быть или не быть – она говорила, многие выступающие это обсуждали. Но все выступления были такие веселые – прямо скажем, тогдашние дни рождения проходили интереснее, чем сейчас. Выступали не какие-то там официальные лица, а преподаватели. Многие из них были известными учеными, и каждый старался пошутить.

— Выступали как живые люди?

— Да, и любили обыгрывать очередную дату. Три года, пять лет, семь лет и так далее. Составные тоже.

— Та самая магия чисел, о которой постоянно говорил Земляков?

— Да, та самая магия чисел. И многие в своих речах желали, чтобы школа не закрылась, потому что всё время ходили эти разговоры: «А это надо? Давайте закроем». Они ходили с самого начала. Валера Пахомов даже рассказывал историю, что когда на Ученом совете МГУ обсуждали то ли еще вопрос об открытии, то ли уже вопрос о закрытии, декан экономического факультета сказал, что у нас уже был один Царскосельский лицей, и мы знаем, что из этого получилось.

— Интересная параллель.

 Старт в науку

— Когда надо начинать заниматься математикой? Всегда ли к математические способности проявляются именно в раннем возрасте?

— По-разному бывает. Например, Колмогоров считал – так, по крайней мере, у меня отложилось – что когда человек старше, он делает более осознанный выбор. Пусть он и пропустил год, но за счет вот этого осознания он успевает за свой единственный год пройти если не столько же, сколько за два года, то на том же уровне и более интенсивно. В том числе и поэтому у нас появились ЕЖи. И они в целом занимались лучше, у них оценки были лучше, чем у двухгодичного потока. Это не единственная причина, это одна из причин – в том, что они более целеустремлённые.

— То есть нет такой зависимости, как с игрой на скрипке, что если тебе в шесть лет руку не поставили, то все, скрипачом не станешь. С математикой не так?

— Нет, не так, или не совсем так. Вот, пожалуйста, прекрасный пример. Будущий филдсовский лауреат Андрей Окуньков учился на экономическом факультете, у Пахомова. Валерий Федорович уговорил его перевестись на мехмат. При этом он попал в так называемый «армейский призыв» и год отслужил. То есть серьезно заниматься математикой начал относительно поздно. В школе на математические олимпиады он не ходил. Но достиг огромных математических успехов.

— У нас одна девочка, Света Братченко, тоже на экономфак поступила, а она по математике в сборной на межнаре была.

— Было время, когда экономфак был престижным, мода такая была. Так или иначе, пример есть. Не тот случай, когда человек уже в школе в старших классах серьезно погружается в математику. Не обязательно в олимпиады: у нас сейчас некоторые ученики ходят в Независимый университет в одиннадцатом классе. Если уж туда ходишь, то это оказывает влияние. Вот Никита Башаев, который турниром юных математиков занимается. Он целый год в Независимый ходил, умных математиков слушал, и выбрал самое, видимо, сложное для изучения математики место – группу при лаборатории Чебышева в СПбГУ. А в биографии Окунькова такого не было. То есть бывает по-разному.

— И в старшем школьном возрасте, и в студенческом еще не поздно заняться математикой?

— Колмогоров подчеркивал, что к своим высшим научным достижениям математики чаще приходят в раннем возрасте. Действительно, Галуа было 19 лет, Паскаль свою теорему о гексаграмме в 16 лет опубликовал, Абелю был 21 год, когда он получил самый известный свой результат и таких примеров много. Многие математики проявили талант очень рано. Сам Колмогоров свою первую работу по тригонометрическим рядам, которая принесла ему международную известность, тоже очень рано сделал, в 19-20 лет. Это, кстати, было одной из причин создания интерната, помимо тех, о которых мы говорили, чтобы как можно раньше детей включать в научную работу. В принципе – да. Но в интернате это на самом деле нечасто работало. У нас было два таких по-настоящему ярких примера. Один – Юрий Матиясевич. Он в 19 лет сделал две работы, опубликованные в «Докладах Академии наук». Второй пример – это Леонид Левин, который у нас учился. Он в десятом классе сделал работу, которую Колмогоров представил в «Доклады». Больше столь же впечатляющих примеров, насколько я знаю, не было. Но были такие, кто рано защитился. Например, Женя Щепин защитил кандидатскую и почти сразу докторскую, вот он рано стал член-корром. Есть еще такие примеры, кто рано становился доктором, но чтобы вот прямо все хором в науку рано шли – такого нет.

— Задача интерната все-таки в том, чтобы вытащить людей, дать им шанс.

— Реально ранний вход в науку слишком от многого зависит. Либо человек должен быть гением, тогда он действительно в науку как ракета влетает, либо должны сложиться обстоятельства, чтобы не только в интернате его пестовали, а и в университете, как только он пришел, в науку дальше двигали. А это не получается. Был одно время эксперимент в 70-е или 80-е, когда на мехмате специально делали группы из выпускников спецшкол – не только из интернатовцев, а и из других спецшкол. Почему-то это не сработало. Думаю, плохо старались. Может быть, надо было слишком радикально перестраивать систему, а этого никто не хочет.

— В наше время, в 80-е, всех равномерно размазывали при распределении по группам.

— Видимо, это была уже реакция на неудавшийся эксперимент. После этого стали размазывать. Теорию можно подвести подо что угодно. Можно подвести теорию под то, что надо размазывать, а можно подвести теорию под то, что надо собирать вместе. Иногда будет работать одно, иногда другое.

— Если в школе ученику придается сильный импульс, то дальше нельзя опускать эту планку, иначе это все бессмысленно, так?

— Не хочется так думать. От самого человека очень много зависит. Импульсом надо пользоваться, а не надеяться, что кто-то будет и дальше поддерживать.

 — Какие принципы обучения математике заложил Колмогоров и как это менялось со временем?

— Трудно сказать. Не очень понятно, что такое принципы, заложенные Колмогоровым, Если говорить о конкретной программе, ее содержании, то она частично сохранилась. Но у нас каждый лектор читает свой курс. Приходит, скажем, с мехмата какой-то уважаемый человек и читает матанализ. Условно говоря, он читает примерно то же, что и на мехмате. Не совсем, конечно, – естественно, он адаптирует курс к школьникам, но ориентируется на свой мехматовский курс, а что там раньше читали по анализу в интернате, ему не столь важно.

— А уровень всегда был высокий? Планка сразу была поднята на уровень младших курсов мехмата?

— Планка поднята была сразу высоко. Но было с самого начала понятно, и чем дальше – тем больше, что лучше не преподавать то, что потом будет преподаваться в университете. Это проблема всех математических школ, и не только у нас. За границей та же проблема. Ученик в школе многое проходит, потом приходит в университет, ему все легко, он думает, что все знает, а все-таки лектор читает тот же анализ как-то по-другому, начинает спрашивать на экзамене так, как он прочитал. Но это даже не самая неприятная вещь. Хуже, когда наш выпускник не учится, вроде как он уже все знает, расслабляется – и вот он первый курс гуляет, а на втором курсе пропускает момент, когда надо было собраться, и возникают проблемы.

— Все-таки в интернате всегда учили больше вширь и вглубь, а не накачивали вперед на программу мехмата?

— Да, конечно. Что касается геометрии, однозначно. Одним из принципов выстраивания моего курса геометрии было то, чтобы этот материал, по возможности, не повторялся в вузе. Если, допустим, на мехмате говорят про матрицы n×n , то у нас 2×2 или 3×3, то есть человек на простом примере, который имеет наглядный геометрический смысл, может познакомиться с тем, что такое матрица, с ее интерпретацией, и в дальнейшем это ему поможет. При этом он не будет думать, что уже все знает про матрицы, потому что n×n он не проходил (хотя, может, и знает). Это называется словом «пропедевтика». Но есть предмет, а именно математический анализ, где трудно провести эту линию.

— Выходит, не так просто сформулировать эти самые принципы, которые ввел Колмогоров и для чего, собственно, школу задумывал?

— Для чего задумывал – это понятно. Научная работа в раннем возрасте и помощь детям из отдаленных мест – это два основных положения, они до сих пор существуют. Научная работа – это тоже не совсем однозначно, далеко не все школьники могут заниматься научной работой. И вообще, что значит – школьник занимается научной работой? Это все сложные вопросы. Но все-таки мы к этому стремимся. Теперь каждый ученик должен сделать некую «творческую работу», и это отвечает замыслу основателей.

— То есть должен прививаться какой-то интерес, кроме натаскивания на поступление?

— Что касается натаскивания на поступление, в то время было на самом деле важно уделять этому достаточно много внимания. И на содержании курсов это отражалось, потому что вступительный экзамен, как известно, был очень сложным. К тому же интернатовцев долгое время вовсе не принимали с распростертыми объятиями. Даже бывало, что им труднее было поступать, типа вы слишком умные там. Смотря к какому экзаменатору попадешь. Правда, потом был период, когда выпускники могли получить рекомендации для поступления, например, на мехмат, но это все зависело от общего конкурса. С конкурсом проблемы – введем эти рекомендации, а если конкурс и так семь-восемь человек на место, то они не нужны. В общем, была необходимость готовить к вступительным экзаменам достаточно серьезно, в том числе по геометрии. Хотя готовить по стереометрии, как выяснялось, почти бесполезно, потому что стереометрические задачи были настолько трудные, что на мехмате, что на физтехе, что подготовить к решению такой задачи можно было только единицы, и то нужно было этой стереометрией заниматься, с утра до вечера каждый день, чтобы подготовиться. А дает она всего одну задачу. Проще все-таки научиться решать остальные пять.

— Вы говорили, что если непонятно, как решать стереометрию, то оставляйте ее на потом. Решайте все, кроме стереометрии, и этого будет достаточно.

— Практика показывает, что многие, даже те, кто хорошо знал предмет, все-таки не ее решили. Я помню класс, где был Стас Барабаш, они тогда ко мне приехали после вступительных экзаменов. Я был удивлен — приехали ко мне туда, где я живу, несколько человек, трое или четверо их было, довольные, что поступили на физтех. Я стал спрашивать, стереометрию-то решили? Говорят, нет, но все равно поступили. Рассказали мне свою задачу, в дальнейшем я ее давал всем – учились, как ее надо решать. Стас один из любимых моих выпускников; он сейчас директор шведского института космических исследований.

Ученики

— Кого Вы запомнили еще из учеников?

— Запомнился самый первый выпуск. С ними контакт есть до сих пор: Володя Годованьчук мне нередко звонит, а его приятель Леня Богачев в Англии, с ним тоже иногда контактирую. Кстати, они оба тоже работали в интернате, у ЕЖей. Еще из этого же класса помню ученицу, на которой впоследствии женился Тарас Лукашенко, когда она студенткой стала. В следующем выпуске ярко запомнились двое. Один из них, Аркадий Вайнтроб, был, да и есть, суперматематик. А с ним вместе сидел на задней парте Прасолов Витя, в будущем автор многочисленных задачников (особенно популярен его задачник по геометрии) и других книг. И так из каждого класса – кого-то больше запоминаешь, кого то меньше. Один мальчик запомнился, потому что получилось, что я его как бы обидел. До сих пор его фамилию помню. Но я его не собирался обижать, я вообще никого стараюсь не обижать. Получилось так, что я разбирал одну работу, которую написали дети, критический анализ провел, не говоря, чья она. Это был «трактат» по теореме Шаля. Когда я закончил разбор, на него это так подействовало, что бедный мальчик весь покраснел и выбежал из класса со слезами на глазах, хотя я его ни разу не упомянул. Я и выбрал его работу более-менее случайно, просто взял сверху пачки, они у меня лежали на столе и вверху были похуже, чтобы было что разбирать; но таких работ было много. После этого я таких экспериментов больше не делал, но этот случай я запомнил. Обычно все-таки больше хороших учеников запоминаешь. Ну, например, в одном классе сидели вместе, кажется, за первой партой Саша Кузнецов, сейчас он Александр Иличевский, известный писатель, можно сказать, знаменитый. Он сидел с Володей Рагулиным, и это была замечательная парта. И Саша был отличный математик и физик, больше даже физик, и Рагулин был ярко выраженный математик, в итоге он Гарвард заканчивал. Как раз тогда начинались обмены с американской школой, это отдельная история, но благодаря ей и своей голове, конечно, он в Гарвард и попал. Еще запоминаются ребята с необычной для наших выпускников судьбой. Например, Сергей Поликарпов. Это был не самый сильный математик, но он не стеснялся задавать вопросы, когда непонятно, а мы таких любим. Он стал хирургом, доктором медицинских наук. Редкий случай. Или Алеша Зубов, один из лучших математиков в своем классе, после окончания мехмата остался на кафедре общей топологии. И вдруг неожиданно узнаю от него, что он переквалифицировался в музыковеды. С несколькими последними выпусками тоже общение продолжается.

Коллеги

— Кого из Ваших коллег Вы хотели бы вспомнить персонально?

— Из коллег это, во-первых, Саша Земляков, мой друг. Правда, я с ним никогда не работал вместе в одном классе, но в одном потоке – да, и в одном классе на разных предметах – да. А главное, что мы жили вместе в общежитиях.

— Он больше в ЕЖах работал?

— В двухгодичном потоке тоже. Но больше в ЕЖах. Если брать первые лет 10 моей работы, назову Сашу Звонкина. Он уже давно во Франции. Сейчас, наверное, для широкой математически ориентированной публики он более всего известен как автор книги «Малыши и математика». Про то, как учить математике детсадовцев, это из его личного жизненного опыта. Кое-что я позаимствовал у него. Конечно, Пахомов, с которым мы много работали вместе. В основном тех, на кого я ориентировался и что-то заимствовал в плане преподавания, какие-то приемы, я назвал.

— А к Колмогорову на лекции вы ходили?

— На лекциях его был, но, как известно, его лекции было трудно воспринимать, у него и дикция была своеобразная. Все это знают. Хотя он тщательно готовился к лекциям – есть известное фото, где он снят в своем кабинете в интернате в процессе подготовки. Может быть, он думал об аудитории лучше, чем она есть. Полушутя говорили, что к нему на лекцию для студентов приходили аспиранты, а на лекцию для аспирантов профессора, чтобы потом объяснять аспирантам. Его лекции – не образец. Образец лекции это был Сосинский. Вот у него и почерк был идеальный, я вообще такого изумительного не видел. (У Землякова, кстати, тоже был красивый почерк.) Как он доску делил на области, здесь писал одно, здесь другое – то есть тоже целая наука. Это я у него позаимствовал.

Если вспоминать, с кем еще я работал… Со многими работал, не хочется никого обижать, можно многих назвать. Подолгу вместе – в паре или тройке – мы работали с Ниной Бовт, Женей Федоровым, а дольше всех – с моим нынешним напарником Юрой Егоровым. Кого ещё надо назвать обязательно – это Андрей Егоров.

— И в «Кванте» ведь вы вместе работали?

— И в «Кванте» вместе, и в жизни вместе. Ездили куда-то вместе. Не знаю, насколько он повлиял, но он был очень ярким человеком, прекрасным лектором.

— Ваши лекции уже тогда были такие четкие, структурированные, понятные – это Вы у Сосинского научились? Все было доходчиво, хотя и не очень просто.

— Что-то почерпнул у него, что-то у Андрея Егорова. Но все-таки главное – собственный опыт, обратная связь с учениками, то есть наблюдение за их реакцией.

Квант

— Давайте еще поговорим о журнале «Квант» в Вашей жизни.

— В «Квант» я пришел благодаря Землякову и благодаря Сосинскому. Земляков как-то очень рано стал отдавать много времени образованию, педагогической работе, он и в интернате работал, и писал статьи в «Квант». Я сначала меньше на это был настроен, но так получилось, что в итоге тоже втянулся. Я видел, как он работает, и это одна из причин, по которой я пришел преподавать в интернат. Он первым и предложил мне статью в «Квант» написать. Она называлась «Шесть доказательств теоремы о медианах». Это был 1978-й год. Земляков знал, о чем я рассказываю на лекциях и уроках, и сказал, что из этого может получиться статья. В результате там мода такая завелась, и потом было, например, «много доказательств теоремы о биссектрисе» и т. д. Удачная получилась статья, читатели ее хвалили. Так я стал писать, писал немало, потом одно время работал редактором. В 90-е годы, когда стал издаваться журнал «Quantum», американская версия «Кванта», я там был редактором по математике на пару с американским коллегой, очень известным деятелем  математического образования; его зовут Марк Сол. И в течение 90-х годов я массу времени этому журналу отдавал.

— Хорошо, что удалось пережить тяжелые времена 90-х.

— Да, «Квантум» действительно помог и материально, и вообще интересно было.

— Журнал «Квант» удалось сохранить, в том числе, и Вашими усилиями?

— Я бы не стал прямо так говорить. Издание «Квантума» действительно помогло продержаться в самое трудное время и «Кванту», и его авторам, но насколько именно это помогло сохранить «Квант», не берусь сказать. Когда все журналы рухнули в 90-е годы после своих миллионных тиражей, тогда и «Квант» вместе с ними рухнул. В советское время «Квант» стоил 40 копеек, и у него тираж был 300 тысяч. А в 90-е годы люди уже стали считать каждую копейку, и даже 40 копеек на «Квант» не готовы были отдать, тем более что, тогда это уже было не 40 копеек. Тираж резко упал. И сейчас он остается маленьким, но все-таки сейчас другое время, сейчас есть интернет, и журнал выкладывается в сеть, появилось много возможностей.

— В «Кванте» был такой интересный художник Павел Иванович Чернусский, знаю его по урокам акварели.

— Да, с Пашей мы дружили; к сожалению, давно с ним не виделись. Некоторые свои статьи я специально его просил проиллюстрировать, и он это делал прекрасно. Была, например, статья «Выход в пространство», сильно расширенный вариант одной из старых статей Игоря Федоровича Шарыгина, из которой я взял идею и несколько задач, а остальное дописал. Получилась совместная с ним статья для журнала «Quantum» о том, как решать планиметрические задачи, рассматривая их как стереометрические или с точки зрения стереометрии. И вот Павел нарисовал к ней такую заставку: некий условный, очень «объемный» человек здоровается за руку со своей тенью, а сам как бы висит над землей. Так он этот выход в пространство художественно преломил. Этим и отличаются «квантовские» художники. Они умудряются, даже не всегда понимая суть статьи, а статьи в «Кванте» действительно очень непростые, как-то рисовать к ним хорошие иллюстрации. Это классно. Вообще графика в «Кванте» – это отдельная тема. «Quantum» дважды удостаивался американской национальной премии за лучшую обложку. Тогда было тяжелое время, и «Quantum» иллюстрировали многие московские художники и графики, причем художники буквально первого ряда.

— В «Химии и жизни» и в «Кванте» тогда были прекрасные иллюстрации.

— Да. Например, Сергей Бархин. Это известный театральный художник, просто один из ведущих московских художников. Или, допустим, для «Квантума» делал иллюстрации Дмитрий Крымов, сын режиссера Эфроса, сам тоже известный режиссер и художник. И раз уж об этом зашла речь, надо обязательно назвать еще Эдуарда Назарова, художника-постановщика фильмов про Винни-Пуха и кучи других замечательных мультфильмов.

Головоломки

— Расскажите еще про ваше увлечение головоломками.

— Оно началось с того, что Андраш Сенеш, мальчик из Венгрии, который у нас учился, привез пять кубиков Рубика вскоре после того, как кубик появился на свет, и один подарил мне. Купить в Москве их тогда было невозможно.

— Да, помню, какой был ажиотаж. Андраш – это как раз наш выпуск 1981 г. Тогда еще в «Кванте» Ваша статья появилась.

— В «Квант» сначала написал статью известный петербургский, тогда ленинградский, математик В. Залгаллер. Это была первая статья, по-моему, вообще в Советском Союзе про кубик. Вскоре после этого появилась статья в «Науке и жизни», и там уже пошла серия статей. Но «Квант» раньше это начал. Автор статьи рассказал про свой алгоритм сборки. А я уже достаточно поиграл с кубиком и написал приложение к этой статье – об инвариантах кубика. Потом уже сам писал статьи. Так, благодаря Андрашу, у меня случилась отдельная страница в жизни – головоломки. Меня нашел  интересный человек, Анатолий Тимофеевич Калинин. Он в то время коллекционировал головоломки. У него было их огромное количество в квартире, все стены уставлены стеллажами с ящичками и в каждом ящичке куча механических головоломок. Он ездил каждый год на международную встречу головоломщиков, туда каждый приезжает с чемоданом одинаковых собственных головоломок, обменивается с другими и увозит домой чемодан разных. Анатолий Тимофеевич предложил вместе написать книжку о математических головоломках, и мы её написали, но без кубика Рубика. Мы планировали, что кубик Рубика будет во второй части, но тут как раз настал 91 год, и все это накрылось. А первая часть имела подзаголовок «Вокруг кубика Рубика», она вышла. Мы взяли из его коллекции кучу головоломок математического плана. Потом он переключился с коллекционирования головоломок на всякие невозможные объекты типа корабля внутри бутылки и всякие другие.

— Головоломки – это хорошие вещи, чтобы привить интерес к математике? Нужно ли их иметь в доме, где растет ребенок?

— Да уж хуже не будет. Кстати, многие задачи по элементарной геометрии на самом деле очень похожи на головоломки. Если же вернуться к моей истории, Калинин меня как-то привел в редакцию газеты «Поле чудес», аффилированной с телепередачей «Поле чудес». Сейчас эта газета уже закрылась, а тогда была популярна, и её редакция задумала привезти команду России на чемпионат мира по головоломкам. Так я три раза съездил на этот чемпионат как капитан (руководитель) команды. Это была первая половина 90-х.

— И какие на этом чемпионате были головоломки?

— Там были головоломки больше для карандаша и бумаги. Первоначально этот чемпионат возник как соревнование по кроссвордам, но поскольку языки у всех разные, то это было не решение, а составление кроссвордов, марафон. Давали 24 часа, и нужно было сочинить самый длинный кроссворд. Участвовали в нем люди от газет, печатающих кроссворды и другие головоломки, такой газетой было и «Поле чудес». Но в какой-то момент финны пожаловались, что из-за особенностей их языка, где слова длинные, им труднее составлять кроссворды, чем, скажем, американцам. И тогда решили проводить соревнования, независимые от языка. Давались задачи типа того, что сейчас называется «судоку». Тогда в России они были малоизвестны. Интересно, что там я познакомился с японцем, который изобрел головоломку «paint by numbers». У нас это занятие, кажется, так и называется – «японский кроссворд». Там тоже сетка и указано число клеточек, которые надо закрасить в каждой горизонтали и вертикали. В итоге получается некий рисунок. Этот японец меня даже несколько раз поздравлял с

Новым годом открытками с головоломками. Он много чего разного придумал. Насчет судоку я не уверен, что это он, но он придумывал другие такого рода вещи. И еще на чемпионате давали решать одну механическую головоломку. Но в основном там писать надо было, в том числе и кроссворды заполнять, только слова в них загадывали картинками. Ну, это тоже отдельная история.

Про компьютер

— Сейчас появилось много обучающих программ, и Вы участвуете в их создании. Как Вы стали заниматься этим?

— В начале 90-х в интернате был обмен со школой Choate Rosemary Hall, это одна из ведущих американских частных школ, ее в свое время заканчивал Джон Кеннеди. Они к нам приезжали на две недели, и наша группа туда ездила. А меня они пригласили персонально в их летнюю школу, это был 91-й год, второй мой выезд за рубеж (первый тоже был в Америку). И они мне там подарили компьютер Макинтош.

— По тем временам это была роскошь!

— Я этого даже не осознавал. Мне было неудобно брать его себе, рука не поднялась отнести его домой, и я его отнес в интернат. А здесь он просто пропал. То есть не то что физически исчез, но толком им никто не пользовался. Надо было мне его все-таки себе взять. На нем была установлена только что вышедшая первая версия программы The Geometer‘s Sketchpad. Это была одна из двух самых первых программ динамической геометрии; они позволяют строить на компьютере чертежи, а потом их «шевелить», сохраняя алгоритм построения. Она мне очень понравилось, как же иначе. Она была ещё относительно примитивна, но все равно было здорово – сама идея и все такое. Через несколько лет появились и другие аналогичные программы, одна из них ко мне попала, французская, на ней я уже довольно много чего делал – рисунки рисовал для публикаций, что-то смотрел – в общем, таким образом я в это дело втянулся. А еще в 97 или 98-м году в фирме «1С» появился отдел образовательных программ, они выпускали обучающие диски. Сначала они выпустили диск по химии (кстати, там главным автором был наш Алексей Галин), а потом, естественно, задумали диск по математике. Тогдашний руководитель этого отдела сделал очень умную вещь – он пришел в «Квант» за авторами. Молодец. Более подходящего места, где бы собирались лучшие математические «образователи», не придумаешь. Чем в какую-то школу идти или в какой-то институт… Это он сделал правильно.

— В «Кванте» была творческая среда? И поэтому туда пришли из «1С»?

— «Квант» – это марка, можно даже ничего не объяснять. Поскольку я как раз этим интересовался, то это ко мне и пришло. И вот мы сделали диск. Назывался он «1С:Репетитор. Математика. Часть 1» (часть 2 не получилось выпустить). Его главной, но не единственной «фишкой» были ролики во флэше (Shockwave Flash), анимация с озвучкой. Это был очень хороший диск, и специалисты оценили его хорошо. Вот так я начал плотно заниматься обучающими программами. Дальше я пропущу часть истории – линию динамической геометрии, начавшуюся с компьютера Макинтош. Она жила своей жизнью и привела к следующему большому проекту в «1С» – диску, составленному из нескольких разделов по разным предметам: алгебре, геометрии (и планиметрии, и стереометрии), теории вероятностей, информатике. Две последние части делали другие люди, а вот алгебра, планиметрия, стереометрия – это было на основе той самой американской программы динамической геометрии, которая тогда уже была в России локализована как «Живая Геометрия». Этот проект тоже всем понравился, это был отличный диск, надо сказать без ложной скромности. Там столько было оригинальных творческих идей! Над ним работали лучшие авторы, а лучшими авторами оказались студенты мехмата. Мой сын, который тогда учился на мехмате, сыграл роль и разработчика, и менеджера. Он пригласил своих друзей. Там у нас учителя тоже были заняты, то есть были и взрослые авторы. Я уже знал после «1С:Репетитора», с кем стоит работать, а с кем нет. Здесь везде сроки, дедлайны, важна еще и трудовая дисциплина. И с учителями тоже приходилось иметь дело. Но после этого я старался избегать сотрудничества с ними, хотя это были хорошие учителя.

— Неужели студенты мехмата оказались более дисциплинированными?

— Дело не в дисциплине, а, во-первых, в их математической грамотности, и во-вторых, в креативности, конечно. Хотя учительнице я тогда поручил тему, где особенно креативить и не нужно было.

— Вы участвовали в создании всех частей?

— Да, я был руководителем этого проекта, как и предыдущего.

— И когда он вышел?

— Он вышел в 2004 году. Он делался по госзаказу, там был тендер, который нужно было выиграть. А потом возможность использовать эту самую «Живую Геометрию» исчезла. Для следующего проекта надо было заплатить правообладателям большую сумму, а денег не было на это. И внутри «1С» родилось предложение – давайте сделаем свою программу. Я стал научным руководителем этой разработки. Мне очень помогла наша выпускница Наташа Лебедева, она тогда работала в «1С»; сейчас, после большого перерыва, опять вернулась. И начали делать. После долгих обсуждений придумали название – «Математический конструктор». Первым программистом был Леша Тарасов, тоже наш выпускник, олимпиадник, замечательный молодой математик, получивший очень интересные результаты. Следующим основным программистом, разрабатывавшим «Матконструктор», стал Руслан Черемин, мой бывший ученик, потом ещё один бывший ученик – Артём Анисимов. Это всё были молодые ребята, а лет 5-6 назад к нам присоединился еще один наш выпускник из старшего поколения, Владимир Булычев. Он соавтор одного из школьных учебников по теории вероятностей и ему принадлежит, в частности, весь вероятностный блок программы. Сейчас он – соруководитель всего проекта.

— Все это сделали наши выпускники?

— В значительной степени. Но всегда кто-то был и из «1С», конечно. У нас всего два программиста было в каждый момент, поэтому мы чисто физически не могли развиваться быстро. Зато это своя программа, ее можно было делать так, как именно нам представлялось правильным. Сначала я сам долгое время предпочитал «Живую Геометрию», я ее тоже очень хорошо знал, а МК на первом этапе еще не был достаточно хорош. Но постепенно, чем больше учитывались пожелания, тем лучше он становился, и сейчас очень удобен.

— В интернате «Математический конструктор» используете?

— Да, в интернате у меня математический практикум фактически состоит из заданий на МК. С моим последним классом мы еще ввели такое понятие – «мини-прак», когда в домашнем задании нужно какую-то картинку нарисовать. Некоторые картинки геометрически очень сложные, их циркулем и линейкой замучаешься рисовать, а здесь быстро, и, главное, можно потом пошевелить, «пощупать».

— Получается более наглядно? Можно лучше прочувствовать?

— Да, и видишь разные случаи, можно и прочувствовать и даже придумать решение задачи.

— У каждого ученика есть своя программа?

— «Конструктор» был коммерческой программой, его надо было покупать, купили лицензию на СУНЦ. Сейчас уже это не надо. Последняя версия бесплатная, изменилась маркетинговая политика.

«Математический конструктор» тоже занимает у меня много времени.

— То есть идете в ногу со временем?

— Стараюсь. Есть еще такая штука, называется МЭШ – «Московская электронная школа». О ней есть разные мнения, но так или иначе это система, содержащая, в том числе, много учебных материалов, которыми могут (а некоторые даже говорят, что и должны) пользоваться учителя математики. У них для этого есть интерактивные доски в классах, они загружают материалы МЭШ и показывают.

— Не во всех школа есть интерактивные доски.

— Все равно есть тенденция к тому, что все учителя должны использовать материалы из этого МЭШа. Так мне объясняли. Я не знаю, как на самом деле, насколько это обязательно. Если нет доски, можно через компьютер, через проектор.

— Там все разделы математики представлены?

— Говорить подробно про МЭШ я не берусь: мы от них получили некий заказ и его выполняем. И совсем недавно в МЭШ уже появились виртуальные лаборатории по математике на основе «Математического конструктора». Если же говорить про «Математический конструктор» и другие аналогичные программы, то не во всех разделах школьной математики они работают одинаково эффективно. Его области применения – геометрия, функции и графики, а также теория вероятностей. Для арифметики, например, это инструмент несколько чужеродный, хотя у нас и есть «арифметические игры». В «Конструкторе» две главные вещи – это создание модели (конструирование) и эксперимент (или исследования). Вот такая деятельность. Арнольд говорил, что математика – это экспериментальная наука, по крайней мере, ему это приписывают. И в МК эта идея реализована. Плохо, когда даешь задачу, и уже все известно, что в ней надо сделать. По шаблону тык-тык-тык – и получил ответ.

— Новые средства помогают в этом?

— Да. Компьютер становится таким инструментом исследования. Это не самоцель, что надо обязательно использовать компьютер. Можно в принципе и на бумаге, но компьютер даёт такие возможности, которые на бумаге не получишь. Или вероятностный эксперимент поставить, как будто случайное что-то смоделировать.

Недавно открылась еще одна возможность для использования «Математического конструктора» – «Кванториумы», сеть учреждений дополнительного естественнонаучного образования которую развивает Министерство просвещения. Им МК интересен как инструмент математического моделирования.

Математическое моделирование

— Расскажите, пожалуйста, об этом новом для нас направлении – математическом моделировании.

— Математическое моделирование в школе – это область, в которую я оказался вовлечен недавно, в 2015 году, и сейчас она бурно развивается. Интересно, как это случилось. Я получил письмо из Штатов с приглашением в оргкомитет международного соревнования по математическому моделированию. Они приглашают, билет покупают, гостиницу и прочее. Первая встреча оргкомитета была в Бостоне. Я терялся в догадках, о чем это и почему я. Но потом я понял. Им хотелось иметь человека из России. Тот, кто это все возглавляет и давно занимается этой тематикой, стал выяснять, кого пригласить. Благодаря моим занятиям динамической геометрией меня знали нужные люди, они и порекомендовали. Так что в школьное математическое моделирование я попал благодаря этому своему увлечению. Сначала я не понимал, что это такое, как команды-участники соревнований умудряются за три дня написать работу на 20 страниц с решением задачи. Мне и 10 страниц полгода надо писать. Постепенно прояснилось. На самом деле, тема оказалась очень удачной и очень актуальной. Есть такие четыре буквы – STEM – «Science», «Technology», «Engineering», «Mathematics». Сейчас еще в эту аббревиатуру вставляют «A», это «Art», получается STEAM. За границей в последние годы STEM – едва ли не самая активно развивающаяся область математического образования. К ней относится и матмоделирование, о котором мы говорим. Особенно популярна оно в Америке и в Китае. Насчет Китая я всегда привожу цифру, которая просто потрясает: в городских соревнованиях по математическому моделированию города Пекина участвует 25 тысяч команд!

— Команд, не школьников?

— Даже если бы школьников, то было бы много, даже с учетом китайских масштабов.

— Там это реально дает какие-то бонусы при поступлении?

— При поступлении, кажется, это бонусов не дает. Они проявляются потом, при устройстве на работу. Но независимо от бонусов образование будет двигаться в эту сторону, и уже двигается. В том же ЕГЭ есть «задачи с практическим содержанием» – пусть и очень примитивные, но все-таки это какое-то приближение к реальной жизни. И вот, попав в этот оргкомитет, я стал пытаться сначала наших ребят к этому подключить. Потом подключил две школы из Новосибирска, потом еще какие-то знакомые школы. Пока ещё у нас не слишком большой масштаб. Начиналось с этого международного соревнования. А в прошлом году мы уже сами устроили целый международный турнир по математическому моделированию, заменивший наше «Математическое многоборье», проведение которого, к сожалению, по разным причинам пришлось прекратить.

— За основу взяли правила международных соревнований?

— Не совсем. Там соревнование проходит так: команда получает одно задание практического характера, разрабатывает что-то, пишет работу на эту тему и посылает на оценку жюри. Аналогичное соревнование входит и в наш турнир, но кроме него есть еще три, более привычные олимпиадникам. Но и они тоже с практическим уклоном. Например, в прошлом году была задача про точную форму треугольного молочного пакета. То есть задача по математике, но с таким жизненным уклоном. Турнир сразу стал международным, в нем участвовала команда из Макао. В этом году они опять приедут. И тайцы приедут, мои старые друзья. И, надеемся, команда из Болгарии.

— Азия сейчас показывает достаточно высокий уровень и большую заинтересованность?
— Да, и именно это направление, моделирование, там очень популярно. Мы сейчас движемся туда же.

— И у нас к математическому моделированию растет интерес?

— Безусловно. Взять хотя бы те же «Кванториумы». Это не только математика, но еще и физика, робототехника и тому подобное. Летом мы провели в Сколково для их преподавателей курсы повышения квалификации, где рассказали о математическом моделировании, о том, какие там бывают задачи. Мы – это объединение двух команд: тех, кто занимается моделированием у нас в школе, и тех, кто занимается «Математическим конструктором» в «1С», а посередине я. Я рассказывал, как с помощью МК можно моделировать нечто из реальной жизни. На заключительном заседании слушатели должны были представлять собственные проекты. Я думаю, не за горами время, когда матмоделирование появится и в школьной программе. Слова «математическая модель» давно произносятся в школе, но скорее просто как название того, что и раньше делали. Решают, например, текстовую задачу, составляют систему уравнений – вот вам уже математическая модель. Так оно и есть, но обычно сама задача абсолютно искусственная. А вот когда ты берешь задачу «с улицы» – совсем другое дело.

— Но пока это будет на уровне дополнительного образования, каких-то кружков?

— Пока, в основном, так. К своему удовлетворению я вижу, что интерес растет. Будет секция математического моделирования на Московской городской конференции проектов, и я уже для них записывал лекцию про матмоделирование, там и с физфака работает парень, который этим занимается. Это один аспект. А другой – это «Кванториумы». Сейчас мы занимаемся с преподавателями, а дальше у нас план делать это у них в летних школах. У них летние школы проходят в хороших лагерях – «Орленок», «Смена» в Краснодарском крае, «Океан» во Владивостоке, и они с удовольствием нас приглашают.

— Идея в том, чтобы вовлечь побольше народу?

— Да, вовлечь народ и подключить их к соревнованиям.

— А потом они будут участвовать в международных соревнованиях?

— В международных мы и так участвуем. Участвуют две команды от страны.

— Их же надо откуда-то брать?

— Совершенно верно. Сейчас у нас есть несколько школ из Москвы, но лучших надо как-то отобрать, поэтому проводим соревнования. Есть соревнование, в результате которого мы отбираем две команды и посылаем их работы для участия. Пока с переменным успехом, могло бы быть и получше, но не все сразу делается.

— Это уже не только в Москве существует?

— У нас участвуют команды из Владикавказа, из Волгограда, из Новосибирска, из Санкт-Петербурга –географически уже широко. Надо еще численность увеличивать, количество участников.

Нужен ли сейчас СУНЦ

— Нужно ли сохранять спецшколы типа интерната? Где еще создают творческую среду для детей и преподавателей?

— Первый вопрос с самого начала вызывал споры, мы его уже касались. И сейчас приходится иногда слышать совсем с другой стороны, со стороны своих же коллег, что СУНЦ – это отжившая форма, сейчас у нас «Сириус» на первом месте, а еще дистанционное обучение. Вот это, дескать, правильно, вот это охват.

Это все замечательно, тут нечего говорить. Все это направлено на те же цели, ради которых создавался интернат, только для более широкой аудитории. Но для отдельного ребенка, попадающего в окружение себе подобных на два или пусть даже на один год, эффект будет совсем другим. И я не думаю, что то, чем мы занимаемся на уроках, можно масштабировать на «сезонную» и заочную формы обучения. То есть я уверен, что наоборот, невозможно. Невозможно заочно воспроизвести общение между учеником и преподавателем.

С другой стороны, сейчас открывается много новых интернатов. И некоторые городские школы устраивают у себя небольшое общежитие и организуют интернатное обучение. Думаю, это результат рейтинговой системы – способ заманить к себе иногородних олимпиадников, заработать рейтинговые очки и получить за это гранты.

— Мы тоже это делаем. Мы же отбираем, в том числе, и олимпиадников.

— Это разные вещи. Мы отбираем, но у нас нет такого, чтобы люди специально занимались затаскиванием, переманиванием, о чем то и дело слышишь. Может быть, для нас это даже и плохо, ведь большинство других школ начинают отбор раньше нас. Если у нас откроется 9-й класс, нам в этом смысле будет проще. Это, по-видимому, и произойдет, когда построят новые здания. Хотя идея 9-го класса мне кажется сомнительной.

— Для математиков это, наверное, хорошо – набирать в 9 класс?

— Были же у нас опыты с 9-м классом, и почему-то они прекратились.

 — В Новосибирске есть 9-й класс.

— Не знаю, как у них получается.

— Там немножко более самостоятельные дети. И Академгородок.

— Там, может быть, и атмосфера немного другая, это все-таки не Москва, где много соблазнов. А что касается заманивания в московские школы, то когда мэр объявляет премию в полмиллиона победителю Всероса и сто тысяч только за участие, то дети едут в Москву просто за деньгами. «А я еду, а я еду за деньгами…»

— В регионах их так не могут поощрять.

— Это тоже большую роль играет. То, что школы борются за олимпиадников, – это факт.

— А мы все по старинке – экзамены для всех.

— И это правильно, по-моему. Льготы ведь у нас тоже есть, они и должны быть, а уж дальше кто что выберет. Олимпиадники уровня национальной команды в любой школе все равно учатся по сути дела отдельно от своих одноклассников; у них постоянные сборы и соревнования. И было бы более или менее все равно, есть они или нет, если бы не два момента. Первый – за них школе дают деньги (впрочем, для нас, благодаря гранту, который дали всем СУНЦам, на ближайшие пару лет это большой роли не играет), а второй – благодаря успехам школы на олимпиадах, в эту школу придут учиться какие-то новые хорошие дети.

— По информатике Елена Владимировна вытаскивает детей.

— Елена Владимировна – редкий педагогический талант. Вот эти наши два выпускника, которые во второй раз подряд победили, уже как студенты, на международном чемпионате по программированию, Владислав Макеев и Миша Ипатов. С первым она занималась с младшего возраста. Но у неё в классе 25 человек, и половина из них едет на Всерос. Ей уже не надо никого заманивать, они сами как пчелы на мед… А вот почему половина математиков не едет на Всерос? И не только от нас, но и от других школ в стране? Потому что это разные предметы. Информатика – это алгоритмы. Алгоритмам можно обучить и натренировать их быстро реализовывать. Что, собственно, Е.В. и показывает. Правда, сказать-то легко, а у других так не получается. А по математике это невозможно. Да, каждый год есть примеры, когда целеустремленные дети за счет труда добиваются успеха на олимпиадах высокого уровня. Только эти примеры единичные.

Про ЕГЭ

— Родители, отправляя детей в интернат, конечно, хотят, чтобы они хорошо написали ЕГЭ, чтобы поступили?

— Что касается ЕГЭ и поступления, с этим, слава богу, проблем нет.

— В этом году Ваш маткласс показал какой-то фантастический результат на ЕГЭ по математике?

— Что-то мне не верится, что результат этого года по ЕГЭ будет когда-нибудь повторен, раньше такого точно не было. Из этого класса девять человек получили 100 баллов, а еще были и 99, и 98… Правда, многие говорят, что в этом году математика была, что называется, «халява». Критерии были те же самые, но сами задачи, может быть, действительно полегче. Ведь эти 100 баллов зарабатываются на самых последних задачах.

— В этом году в среднем по стране процентов на двадцать больше 100-балльников?

— Я этой цифры не видел, но если в среднем на двадцать, то у нас получилось в разы больше. В прошлом выпуске было двое или трое 100-балльников. В этом в три раза больше, именно в этом классе. Самое приятное, что специального решения этих ЕГЭшных задач у нас не было – по крайней мере, у нас на геометрии. То есть мы проходим свою программу, по ходу дела, конечно, обращаем внимание, что такие задачи бывают на ЕГЭ, но целенаправленного натаскивания не было. А то, что оно есть во многих других местах — это точно.

— Многие школы занимаются натаскиванием на ЕГЭ, а у нас в этом году и без того получился хороший результат? В этом, наверное, и есть разница между интернатом и прочими школами?

— Только добавим – не единственная. Я некоторое время работал в одной московской школе, не из самых топовых, но такая крепкая хорошая школа, известная в Москве. Там учителя должны в 10-11 классе готовить к ЕГЭ, это их цель. Этого требуют от них и родители. У нас в матклассе подготовка к ЕГЭ никогда не была самоцелью не только на геометрии, но и на анализе. На алгебре, по идее, это должно было присутствовать в большей степени, но насколько я знаю, и там тоже не было такого, чтобы дети весь год готовились к ЕГЭ. Так что получилось здорово. У информатиков, где мы тоже ведем, результаты по ЕГЭ нормальные, но не сверхъестественные. Информатики что-то совсем помешались на этой своей информатике и математикой плоховато занимались. Хотя бывает, что и они показывают хорошие результаты. Один парень, победитель международной олимпиады, когда был свободен от своих бесконечных информатических сборов, всегда приходил на математику с большим интересом и с удовольствием все решал. Но были и те, которых, видимо, уже не хватало ни на что, кроме информатики.

— Хотя информатам, как никому другому, математика нужна.

— Конечно. В принципе наши информаты, если сравнивать с учениками других школ по стране, по математике стоят гораздо выше, но внутри нашей школы, по нашему гамбургскому счету, они недостаточно активно работали. Был в этом же информатическом классе другой мальчик, он хоть на межнар и не поехал, но в сборной по информатике был и, тем не менее, стал призером Всероса по математике. Ну приезжают к нам умные ребята, что поделаешь.

 — Родители, выбирая школу для детей, часто ориентируются на то, какие показатели у школы по олимпиадам, по ЕГЭ. Наши высокие результаты – не натаскивание, а следствие качественного изучения математики?

— Смею надеяться, да. Если говорить, допустим, про наши классы химико-биологического отделения, то, наверное, там занимаются и натаскиванием в какой-то мере, и это было бы оправдано, но это надо у них спрашивать.

— Некоторых детей родители забирали из интерната именно для того, чтобы получить медаль или конкретно натаскать на ЕГЭ.

— Неразумно. Жизнь длинная, и потом все равно бы у них все получилось хорошо. Есть статистика. Конечно, одного человека, который вдруг почему-то не поступил, статистика не утешит, но это может случиться при любой системе, хоть натаскивай, хоть не натаскивай. Здесь главное другое. Вот в этом же нынешнем математическом классе был еще один парень, который просто поставил себе цель, что ему надо попасть на мехмат. И поэтому он участвовал во всех этих нескончаемых олимпиадах типа «Покори Воробьёвы горы» и готовился целенаправленно, в итоге у него тоже 100 баллов по ЕГЭ. Он просто сам в это вложился. Может быть, если бы он сам не вкладывался, а надеялся только на то, что ему дадут на уроках, так бы не получилось. Он действительно постарался. И он один из немногих, кто наш школьный выпускной по математике написал тоже на полный балл.

— Значит, нам ЕГЭ не мешает, хотя многие его ругают.

— Когда только собирались учреждать ЕГЭ как обязательный для всех, у меня были опасения, что это на нас отрицательно скажется, потому что любой учебный процесс заканчивается экзаменами и всегда как-то подстраивается под эти экзамены. Как бы ты ни хотел, все-таки ты должен иметь это в виду. Даже не тебе это надо, не преподавателю, а ребенку, ученику – ему же надо дальше, ему надо показать хороший результат, а значит, ты должен позаботиться, чтобы у него получилось. Было непонятно, не придется ли сворачивать какие-то наши «полеты на другие планеты» и концентрироваться на рутине – в зависимости от того, какой бы это был ЕГЭ. Слава богу, обошлось. Во-первых, благодаря системе с олимпиадами, которая, правда, тоже уже гипертрофирована и превращается в свою противоположность. 1000 олимпиад – это плохо. Дети, вместо того, чтобы учиться, бегают по этим олимпиадам. Если бы количество олимпиад было более разумным, претензий бы не было совсем. Это плюс, ведь некоторые дети действительно экзамены пишут плохо. Во-вторых, сам ЕГЭ по математике достаточно разумный. На него жалуются, что люди знают, что задача номер пять будет про это, а номер шесть про то, и готовят «по номерам», вместо того, чтобы просто математике учить. Но у нас этой проблемы нет. Для нас есть какие-то темы – то, что надо уметь, – и мы это проходим, дети это знают и в итоге хорошо сдают. В то же время, у ЕГЭ есть плюсы – особенно то, что это независимый экзамен. Но до совершенства далеко.

— Получается, в интернате детей учат просто нормальной математике, а дальше как пойдет: у кого-то олимпиады лучше получаются, у кого-то ЕГЭ?

— Это главная идея. Нам не только не пришлось как-то подстраиваться особо под ЕГЭ, а даже получилось в меньшей степени подстраиваться, чем это было раньше – вспомним хотя бы то, что я уже говорил о зубодробительной головоломной стереометрии.

— Вы считаете, ЕГЭ не такое уж и зло?

— Ну да. Из-за того, что снизился уровень требований на экзамене, не нужно так много времени тратить на бессмысленную отработку, допустим, тригонометрических уравнений, которых нет ни в жизни, ни в математике. Когда-то Земляков умел находить объяснения, почему надо заниматься этой «наукой», тренироваться в решении всевозможных типов уравнений. Вроде того, что когда в университете придется, например, интегрировать, то будут использоваться такие же алгебраические преобразования как при решении уравнений. Но, собственно, а интегрировать-то зачем, когда есть таблицы, а сейчас – мощные математические программы? Тоже большой вопрос. И тогда можно за счет освободившегося времени рассказывать какие-то более интересные вещи. В последние годы я так и делаю. Но всегда подкрепляю «интересные вещи» обычными задачами.

— Получается, что для преподавателя свободы стало больше?

— У нас да, а в массовой школе, скорее всего, меньше, потому что раньше от «обычного» школьного учителя никто не требовал поступления, допустим, на физтех и обычно эту проблему решали за счет репетиторов. А сдавать ЕГЭ нужно всем. Конечно, есть базовая и профильная математика, но сейчас такой ученик пошел, что он и базовый уровень сдать не может. Можно только посочувствовать этим учителям.

Олимпиады

— В этом году у нас всплеск получился не только на ЕГЭ, но и на олимпиадах по математике, этого не было несколько лет. Это случайность или результат целенаправленной работы?

— И не только на олимпиадах: зимой наша команда участвовала в ТЮМе – Турнире юных математиков в Санкт-Петербурге и поделила 1-е место. Причем мы вообще первый раз туда поехали и это не были записные «олимпийцы». С командой работали наши молодые ребята – наш выпускник Никита Башаев молодец, мы приняли участие в турнире по его инициативе, а еще Вася Некрасов, который совсем недавно пришел к нам. Летом мы ездили на международный турнир, но там выступили не столь удачно. Там уже сказалось и то, что английский у нас не очень. Пусть это и не самая главная проблема, но она есть. Когда нужно общаться с другими участниками при оппонировании, рецензировании, а языком не владеешь в достаточной мере, это непросто.

Если же говорить про олимпиады, особенно про Международную математическую олимпиаду, то, конечно, это здорово, что у нас такие ребята – два золота у команды и оба у наших учеников, но, в отличие от успехов на ЕГЭ и в ТЮМе, приписывать этот успех только нашей школе, нашей работе неправильно. Один сильный парень пошел к нам по каким-то своим причинам, он сам из Петербурга, потом переехал в Москву и пошел к нам. А другой парень из Астрахани, оттуда всегда набирают в интернат, и он попал по набору. Нам повезло, что там родился и вырос такой парень, мы же не можем ни родить его, ни готовить к олимпиадам, пока он к нам не приехал. Хотя у нас и есть заочная школа, но она совершенно по-другому работает. К 10-му классу будущие кандидаты в национальную команду уже в основном известны, и с ними ведется целенаправленная подготовка специально обученными людьми. Наша задача, как я ее вижу, — не подстраиваясь под них, сделать так, чтобы учеба у нас была им интересна и полезна, чтобы они чувствовали себя комфортно и не мешали остальным. Тогда они будут охотно к нам идти.

А вот уровень олимпиад чуть пониже – это уже наша заслуга. И в этом, и в прошлом году были ребята и девушки, которые раньше никогда не были кандидатами в международную команду, хотя и участвовали в разных олимпиадах, и когда поступали к нам в СУНЦ, то даже не были участниками Всероссийской олимпиады. А у нас благодаря занятиям на кружках они все-таки выучивались и в конце концов становились призерами Всероса. Вот это мне даже приятнее, чем когда приходит кто-то очень сильный и выигрывает, будучи нашим учеником, – хотя это, конечно, тоже приятно.

— То есть количество всеросников — это уже заслуга нашего интерната?

— Оно не такое уж и большое по математике, но какое-то есть. Здесь ещё большой вклад Алексея Пономарева и его команды, которые много занимаются с олимпиадниками вне стен интерната и они, благодаря этому, узнают, что у нас им будет хорошо.

— Всерос – это уже очень хорошо.

— Безусловно, хорошо. Если же брать вообще всякие олимпиады, то их сейчас развелось очень много и у нас полно призеров всех этих олимпиад. Но вот другой пример. На последнем уроке в день последнего звонка мой коллега Юра Егоров устроил в матклассе опрос: «Назови пять слов, которые характеризуют интернат». Одним из самых популярных «слов» стало имя одного их соученика – Вадима Горева, харизматической личности в классе. Так вот, ещё в начале учебы он как-то заявил, что «презирает олимпиадное движение», так прямо и сказал. Но зато у него склонность к научной работе. Он молодец, очень хороший парень, и делал исследовательские работы, выступал с докладами.

Развитие математических способностей

— Математические способности – это дар или труд? Что дается от природы и чего можно достичь трудом?

— Собственно способности – это дар. Математические способности, как я считаю, это действительно пример тех способностей, которые даруются. В контексте олимпиад, если посмотреть на официальный список, там 24 всероссийских олимпиады. Среди них мы увидим математическую, физическую, химическую, информатическую. А есть и олимпиада по предмету ОБЖ, олимпиада по предмету физкультура (но это не спортивное соревнование). Мы говорим: олимпиада – это соревнование, выявляющее, у кого больше способностей. По крайней мере, так изначально было, что олимпиады выявляли талантливых детей. А какие такие природные способности эти олимпиады выявляют? Вот есть олимпиада по экономике. Наши два мальчика, хорошие математики, пошли на эту олимпиаду, особенно к ней не готовясь, просто посмотрели, какие там бывают задачи, и стали призерами.

— Без специальной подготовки, просто как следствие их общего развития?

— Ну да. Экономические способности, наверное, все же бывают – например, у известных бизнесменов, которые среди наших выпускников, как известно, тоже есть. Но олимпиады же не про это. Короче говоря, математические способности, безусловно, есть, и они проявляются у человека, и это можно выявить, но без труда они не реализуются. Ничего оригинального.

— А если говорить не только об олимпиадах, а о математическом складе ума в целом?

— То же самое. Никто из ученых, специалистов-психологов не будет отрицать, что есть такие способности. Их можно развивать или, наоборот, загнобить. Другой вопрос – получить важные математические результаты, теоремы доказать. Тут одних способностей недостаточно.

— Какова роль учителей, когда приходит ребенок, у которого однозначно есть способности? К нам в основном именно такие дети попадают.

— Тут вопрос, зачем вообще все это нужно, но его мы трогать сейчас не будем. Одна из главных целей нашей школы и других подобных школ – готовить людей, которые потом займутся наукой. Особенно это относится к нам, потому что у нас интернат, а где-то есть способные дети, у которых иначе не было бы такой возможности (по крайней мере, так было в старые времена). Мы даем возможность проявить себя, поступить в университеты и дальше заниматься наукой. Человек, который к нам приходит, имеет два преимущества, которых у него не было бы, останься он дома. Во-первых, он попадает в соответствующую атмосферу, то есть вокруг него такие же ребята, и он себя комфортно чувствует. Не всегда, некоторые уезжают. Но те, кто доходит до конца, вроде бы себя комфортно чувствуют, и их подавляющее большинство. Потом они с удовольствием возвращаются, приходят в школу – и просто так, и помогают, например, олимпиады проводить. Значит, они себя здесь хорошо чувствовали, могли заниматься тем, что им нравится и жить так, как им нравится. Атмосфера, в которой люди, хорошо решающие задачи, пользуются уважением – это очень важно. Второе – это то, что мы действительно не зависим от общих программ.

— Значит, в интернате осталась свобода преподавания и творчества?

— Все так. И коллектив у нас тоже в целом неплохой. У меня много друзей не только на кафедре математики, но и на других кафедрах. Хотя с физиками, например, мы всегда работали по разным дням недели.

— Кстати, это одна из старых традиций, которая осталась – физические и математические дни.

— Она имеет свое объяснение. Так получилось, потому что сначала почти все были совместителями, и надо было какие-то дни им освобождать целиком. Пришлось развести математику и физику.

Раньше и теперь

— Каков уровень детей в начале Вашего преподавания и сейчас? Сопоставимый?

— Этот вопрос часто задают. Я думаю, что в среднем раньше уровень был выше. Взять, к примеру, участие в международной олимпиаде. У нас тогда практически каждый год в команде было 2-3 человека – как правило, победители, призеры. Почему так получилось, понятно. Когда школа только создавалась, она была единственной на всю европейскую часть России и Белоруссию – именно школа-интернат, которая может собрать людей из разных мест. В Москве были свои отличные школы – в разное время разные школы лидировали среди ФМШ – то 2-я, то 57-я. Сейчас даже трудно сказать, какая – и эти, и 179-я. И, конечно, они тоже были очень сильные, но они брали москвичей, а мы москвичей не брали, только как исключение. Единственный москвич был как раз в классе, где я учился, он был сыном зам. редактора газеты «Вечерняя Москва», там была какая-то сложная семейная обстановка. Он жил в общежитии, его приняли в порядке исключения, но он продержался только полгода, хотя и очень хороший был парень. А потом долгое время не было москвичей.

— В каждом выпуске были люди, которые уезжали из-за трудностей.

— Я хочу сказать, что из Москвы мы не набирали. По количеству молодых математических талантов Москва вполне могла сравниться со всей остальной страной.

— То есть раньше уровень был выше, потому что собирали лучших детей со всей страны фактически в один интернат, а теперь они «размазываются» по многим школам?

— Именно так с той оговоркой. что интернатов было четыре и каждый набирал со своей территории. Когда начинают считать – тут столько-то международников, там столько-то – все эти результаты обеспечиваются а) отбором, б) натаскиванием. Конечно в отношении олимпиадных задач «натаскивание», может быть, не самое лучшее слово, но все-таки применимо, потому что это как спортивная подготовка. Она начинается в кружках не позже 5-6-го, в крайнем случае, с 7-го класса. В 7-м классе много этих ребят, постепенно они проходят через «отборочное сито» с суровыми условиями, и в конце остаются те, кто хорошо выступает на олимпиадах – что еще не значит, что они потом станут крупными математиками. Хотя надо сказать, очень многие современные выдающиеся молодые математики, в том числе филдсовские лауреаты, были участниками международной олимпиады, их недаром отбирали. А сейчас мы не можем так отбирать. Когда они к девятому классу подходят, уже почти всех отобрали и разобрали. Почти, но тем менее не всех. С этой точки зрения, естественно, общий средний уровень снизился. Ну и потом, раньше все классы у нас в интернате были одинаковые, физико-математические. Бывало, что какой-то класс оказывался сильнее – так получалось, что туда больше пришло математиков, но в принципе во всех классах были сильные математики. А сейчас мы набираем один математический класс. В других классах математики тоже есть, но на этом уровне буквально единицы. Это не плохо и не хорошо, просто это совершенно другая ситуация, сейчас изменились социальные запросы. Стали больше нужны химики и биологи. Биологи, может быть, даже в большей степени, они важнее для медицины. Математиков-то хватает. Великих математиков так много не надо.

— Но математическая подготовка ведь нужна всем – и химикам, и биологам?

— Безусловно, и математическую подготовку им дают. Но ожидать от них каких-то математических супердостижений мы не можем. Хорошо, что на «маткласс» все-таки набирается, и есть этот более или менее математический класс, плюс ещё информатический, где тоже бывают сильные математики.

— А что изменилось в Вашем курсе?

— Компьютер многое изменил, даже не столько какой-то софт, а просто наличие компьютера все упростило. Когда-то в свое время мы домашние задания от руки писали или на машинке печатали. Печатаешь 6 экземпляров, раздаешь или вешаешь куда-то. Сейчас все проще. Сейчас набрал задание, разослал по электронной почте – и все. Появилась возможность и конспекты лекций раздавать. На каком-то этапе мои всякие закидоны в более сложные темы уже перестали заходить. Кое-что я читал, но потом в экзамен не включал. А как стал рассылать конспекты – ситуация поменялась, теперь и сложные куски дети могут прочитать и понять. Я их включаю в экзамен, и сдают нормально.

— Вы прямо конспекты рассылаете?

— Я не сразу рассылаю, по истечении некоторого времени, чтобы все-таки сначала они сами потрудились, потому что если сразу рассылать, то они могут подумать, что на лекции в принципе можно не ходить. Заставить всех всегда ходить не удается, есть добрый врач. Но ко мне на лекции все-таки ходят. Единственное, раздражает, когда информаты приходят со своими ноутбуками и сидят, уткнувшись в них.

 — И Вы не запрещаете это?

— Я не люблю ничего запрещать. Я их ругаю, говорю – закройте. Они закрывают, а потом опять открывают. Другое дело, что я знаю, что некоторые иногда в это время делают задание по геометрии, которая будет следующим уроком, просто не успевают. Стараюсь утешиться этим, думать о них хорошо.

— Мы тоже, бывало, на геометрии книжки читали по литературе. Одна книжка на класс попадет, и надо было всем успеть.

— Это понятно. Вот когда они «прогают», как они говорят, это уже плохо. По мне так: не хочешь – иди в другое место прогать, но не раздражай человека, то есть меня. Это просто неуважение, когда так себя ведут на лекции. А надо уважать. Я вот их уважаю.

— Наверное, сейчас дети приходят по-другому подготовленные?

— Да. Многие занимались в кружках, летних школах, ФМШ на местах, знают больше чем раньше. Да и учебники у них другие. Значит, то, что ты раньше рассказывал, нужно адаптировать. В какой-то момент я пришел к выводу, что нет смысла возиться с этими меняющимися учебниками. Лучше сделать в курсе такие модули, в которые надо только на входе подать какую-то информацию, а дальше можно не зависеть от того, какой был учебник, система аксиом. В такой системе дальше важно только то, что на выходе – или вступительные экзамены куда-нибудь типа физтеха или МГУ, или ЕГЭ. С ЕГЭ стало лучше, потому что уровень ЕГЭ в целом ниже, чем требования вступительных экзаменов на мехмат или на физтех.

— То есть сейчас сдать профильный экзамен по математике на 100 баллов не так сложно, как было сдать на пятерку вступительные экзамены на мехмат?

— Однозначно. С одной оговоркой – смотря за что ставили пятерку. Полностью решить ЕГЭ проще, чем полностью решить вступительные задачи мехмата. На ЕГЭ для 100 баллов еще и не обязательно решить вариант полностью. Но и на мехмате бывало, что пятерку ставили за четыре с половиной задачи, или за пять с половиной, где «половина» чёткого определения не имела – так было удобнее приемной комиссии.

— Что вообще изменилось за эти годы в концепции школьного математического образования?

— Интересный вопрос. На протяжении этих лет сменилось уже несколько эпох в образовании. Когда я только начал работать, была эпоха Колмогорова, она существовала ровно десять лет. Люди поступили в школу, проучились по этим учебникам – и все. Это еще одна отдельная история, о которой много где можно прочитать. Учебники Андрея Николаевича, главным образом геометрию, раскритиковали, и это, к сожалению, сказалось на его здоровье. Потом пошла другая эпоха, было очень забавно наблюдать, как это сказывается на вступительных экзаменах. Сейчас ЕГЭ – это третья эпоха.

— А после Колмогорова какая была эпоха?

— Для меня это просто были другие учебники, в частности, по геометрии – учебники Погорелова, Атанасяна, по которым учились приходящие к нам дети. Мне трудно четко сформулировать, что конкретно менялось в системе математического образования. На мой курс эти изменения повлияли, но косвенно, как один из факторов, его формировавших. Впрочем, в последние годы в связи с разработкой разных электронных учебных пособий мне пришлось более предметно познакомиться с современными тенденциями в образовании.

В интернате мы жили в замкнутом мире, особенно до введения ЕГЭ. У нас одно, вокруг нас другое. Мы практически никак не зависели – и сейчас мало зависим – от окружающей математическо-образовательной среды. Мы зависим только в том, что детям на выходе надо набрать тем или иным путем определенное число баллов при поступлении. Поэтому мы преподаем то, что хотим.

— В наше время это дорогого стоит.

— Совершенно верно. Если нам удается обеспечивать нужные баллы, то и слава богу, а что там посередине – мы сами решаем, никто не вмешивается. Это одна из причин, почему здесь так комфортно работать. Есть и другая причина, наверное, главная – это дети. С ними приятно общаться, они дают какую-то энергию. А я у них энергетический вампир. Шучу. Ну сидел бы я дома на пенсии, как гриб-мухомор. Конечно, это совсем другое дело.

— Это все-таки взаимный обмен энергиями? Вы же им тоже что-то даете?

— Надеюсь, что да, пока еще получается.

— Закончим на этой оптимистической ноте. Большое спасибо за интересную беседу!

 

Беседовала Светлана Твардовская (выпуск 1981 г., ученица В.Н. Дубровского)

Авторское право © 2019 СУНЦ МГУ Все права защищены.