Естественнонаучное пятиборье — это турнир, в котором разыгрывается 5 задач (по одной от каждого предмета, изучаемого на ВС). Зачитывается условие задачи, и несколько минут дается на обсуждение. Команда, готовая дать ответ раньше, поднимает табличку со своим названием. После ее ответа любая команда, желающая дать альтернативное решение, дополнение к решению или комментарий, может это сделать. Жюри распределяет 20 баллов за задачу по всем участвовавшим в обсуждении командам соответственно их вкладу. Если ответ 1-й команды был исчерпывающим, то она получит все 20 баллов. За пересказ того же решения другими словами команды баллов не получают, за замечания не по делу – тоже, только за действительно ценные и корректно сформулированные мысли. За оскорбление другой команды в своих речах команда может быть оштрафована снятием до 5 баллов. К счастью, такого не случилось!
Задача 1 (информатика)
Один смелый рыцарь попал в плен к султану. Султан повелел запереть рыцаря в тюремную камеру и велел, чтобы в камере вместе с рыцарем постоянно присутствовало два надсмотрщика, один из которых всегда говорит только правду, а второй только ложь. В камере было две двери, вход в одну означал «вечное рабство», а в другую «свобода». Султан поставил условие, что рыцарь должен выбрать одну из дверей, и если он выберет «свободу», то султан его отпустит. При этом рыцарь имеет право задать только один вопрос любому из двух надсмотрщиков (не один каждому, а только один на двоих надсмотрщиков). Рыцарь не знает, кто из двоих говорит правду, а кто лжет. Надсмотрщики, конечно, в курсе, какая дверь ведет на свободу. Какой вопрос должен задать рыцарь любому из надсмотрщиков, чтобы точно определить, какая дверь означает «свободу»?
Задача 2 (физика)
Обруч катится по поверхности. Перед тем, как упасть, он поворачивает. Почему?
Задача 3 (математика)
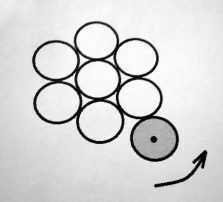
Семь равных кругов расположены так, как показано на рисунке: каждый из шести касается двух соседних, и все они касаются седьмого. По ним катится без проскальзывания восьмой круг такого же радиуса. Сколько оборотов совершит восьмой круг перед тем, как вернется в исходное положение?
Задача 4 (биология)
Всем известно, что растения, водоросли, некоторые протисты и бактерии умеют фотосинтезировать, то есть превращать энергию солнечного света в энергию химических связей. А могут ли животные использовать фотосинтез? Предположите, к каким группам относились бы такие животные, как и для чего они бы использовали фотосинтез?
Задача 5 (химия)
У вас в наличии есть следующие вещества: Ca(NO3)2, Na2CO3, NaCl, Mg. Получите из них максимум новых веществ. Возможно использовать воду в качестве дополнительного реагента, а также любые физико-химические процессы в рамках здравого смысла. Укажите условия проведения реакции.
Командный зачет:
| мат | физ | инф | био | хим | сумма | место | |
| СССР | 20 | 20 | 1 | ||||
| Золото-Время-Восток | 0 | 5 | |||||
| Ерундограф | 2,5 | 2,5 | 3 | ||||
| Движение вверх | 2 | 2 | 4 | ||||
| Интеграл | 0 | 5 | |||||
| Теорема без у | 8 | 6 | 14 | 2 | |||
| 7 — я | 5 | 5 | 4 | 14 | 2 | ||
| Снежарики | 0 | 5 |