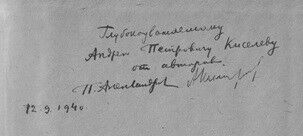В.В. Вавилов
 Андрей Николаевич Колмогоров (1903 – 1987) – один из великих русских ученых, крупнейший математик ХХ столетия, гуманист, патриот, Герой Социалистического Труда, Лауреат Государственной и Ленинской премий, кавалер семи орденов Ленина, академик Российской академии наук и других наиболее престижных академий мира, почетный профессор множества университетов. Как пишет в замечательной книге [1] его ученик, профессор Московского университет В. М. Тихомиров, он «был из тех великих людей, чье соприкосновение меняет направление и в науке и в жизни, кто закладывает первый камень в фундамент, на котором возводится огромное строение, кто сажает в землю росток, порождающий исполинское дерево». Об исключительности роли А.Н. Колмогорова в истории математики довольно эмоционально в книге [3] пишет другой его ученик, академик РАН Арнольд В.И.: «Колмогоров – Пуанкаре – Гаусс – Эйлер – Ньютон: всего пять таких жизней отделяют нас от истоков нашей науки. Пушкин заметил как-то, что он оказал на юношество и российскую словесность больше влияния, чем все министерство народного образования, несмотря на полное неравенство средств. Таким же было влияние Колмогорова на математику».
Андрей Николаевич Колмогоров (1903 – 1987) – один из великих русских ученых, крупнейший математик ХХ столетия, гуманист, патриот, Герой Социалистического Труда, Лауреат Государственной и Ленинской премий, кавалер семи орденов Ленина, академик Российской академии наук и других наиболее престижных академий мира, почетный профессор множества университетов. Как пишет в замечательной книге [1] его ученик, профессор Московского университет В. М. Тихомиров, он «был из тех великих людей, чье соприкосновение меняет направление и в науке и в жизни, кто закладывает первый камень в фундамент, на котором возводится огромное строение, кто сажает в землю росток, порождающий исполинское дерево». Об исключительности роли А.Н. Колмогорова в истории математики довольно эмоционально в книге [3] пишет другой его ученик, академик РАН Арнольд В.И.: «Колмогоров – Пуанкаре – Гаусс – Эйлер – Ньютон: всего пять таких жизней отделяют нас от истоков нашей науки. Пушкин заметил как-то, что он оказал на юношество и российскую словесность больше влияния, чем все министерство народного образования, несмотря на полное неравенство средств. Таким же было влияние Колмогорова на математику».
В математических науках и её приложениях А.Н. Колмогоров сделал так много, что только сухое перечисление направлений его научной деятельности впечатляет. Он активно работал практически во всех областях математики, открывая новые направления исследований, является создателем теории вероятностей и математической статистики. Говоря о своей жизни, научной и педагогической деятельности он подчеркивал: «Я жил, всегда руководствуясь тем тезисом, что истина – благо, что наш долг – её находить и отстаивать….».
Не имея возможности на страницах нашего журнала рассказать о научных достижениях Андрея Николаевича Колмогорова, мы ограничимся здесь только некоторыми фрагментами его огромной педагогической деятельности и, более точно, на его работе в качестве учителя математики. И начнем с истоков – его личного опыта обучения, которое оказывает огромное влияние на каждого педагога и учителя, на его педагогическое творчество в будущем.
- А.Н. Колмогоров пишет (см. [3]) в своей автобиографии: «Родился в 1903 г. в г. Тамбове. После смерти матери Марии Яковлевны Колмогоровой (1903) воспитывался и был усыновлен её сестрой Верой Яковлевной Колмогоровой. Отец мой, Катаев Николай Матвеевич, до революции был агрономом, затем чиновником в департаменте земледелия, после Революции – сотрудником Народного комиссариата земледелия. Умер в 1919 г. В моем воспитании участия не принимал».
Раннее детство, вплоть до переезда в Москву Андрей Колмогоров жил, рос, воспитывался и развивался в родовом имении в селе Туношна в Ярославской губернии под присмотром тетушек – сестер своей матери.
О том, как учили маленького Андрея, написал (со слов А.Н. Колмогорова) в своей книге [1] В.М. Тихомиров: «Никакого букваря, — рассказывал он мне, – не было. Не было такого, чтобы сначала была буква «Б», а потом «А», потом слово, составленное из тех букв, которые изучались ранее. Я смотрел, как читают старшие, и научился читать. Среди первых книг были «Четыре книги для чтения» Л.Н. Толстого. Хорошо помню, как мне читали Сельму Лагерлёф «Рассказы о Христе»…. Потом многие рассказы Лагерлёф Андрей Николаевич читал сам, очень рано прочел «Евангелие», вспоминались ему «Алёнушкины сказки», «Каштанка», «Белый пудель», чуть позднее – «Маленькие дикари» Сетон-Томпсона, «Русские сказки Афанасьева были, но особенных воспоминаний у меня они не оставили. А вот былины русские – об Илье Муромце, Святозаре – начал воспринимать довольно рано. Ну и сказки Андерсена, конечно. И, разумеется, пушкинские сказки».
«В нашем доме под Ярославлем – пишет А.Н. Колмогоров в [4]- мои тетушки устроили маленькую школу, в которой занимались с десятком детей раннего возраста по новейшим рецептам педагогики того времени…». В этой домашней школе издавался журнал «Весенние ласточки», где было опубликовано и первое математическое «открытие» маленького Андрея, подметившего закономерность:
1=12
1+3=22
1+3+5=32
1+3+5+7=42,
………………..
Кроме того, он туда же он поставлял и придуманные им самим задачи. Андрей Николаевич всегда помнил (см.[4],[1]) некоторые из задач из этого журнала: «…была задача о пуговицах: Сколькими способами можно пришить пуговицу? Пуговицы должны были сами себе пришивать. Так что задача, так сказать, происходила «из практики». Мне особенно нравились два способа: из двух параллельных черточек и крестиком. Вообще-то довольно много способов… Естественно, чтобы все дырочки были использованы: прямоугольный треугольничек с пустой дыркой не признавался, конечно. Были и более стандартные задачи о встрече. Я помню, с картинкой было о путниках, идущих навстречу, но, по-видимому, не выходящая из пределов вполне стандартных задач: где два путника встретятся. Я запомнил потому, что картинка была. Я рисовал: два домика, речка, путники идут по дорожке. Потому так ясно и помню до сих пор. Кажется, была логически неинтересная задача».
- Гимназические (1910-1920 с перерывом) годы А.Н. Колмогоров провел в московской частной гимназии Елены Альбертовны Репман и очень этим гордился. В этой гимназии было совместное обучение мальчиков и девочек, что было большой редкостью в те годы. АН. Колмогоров гордился необычностью этой школы, присутствующим в ней духом свободы и принятыми там педагогическими методами обучения и воспитания, многими учителями, которые всячески старались поддержать и развить различные творческие начинания учеников. В гимназии училось совсем немного учеников, но среди ей выпускников несколько видных ученых и профессоров. В этой школе у Андрея Николаевича сложились первые дружеские связи. В этой школе училась и будущая его жена – Анна Дмитриевна Егорова.
Предоставим слово В.М. Тихомирову, который в своей книге [1] приводит многие фрагменты из жизни А.Н. Колмогорова в гимназические годы, которые он описал, в первую очередь, на основе рассказов и воспоминаний самого А.Н. Колмогорова.
«В основном учителя гимназии Репман были очень опытными педагогами. За одним исключением – молоденькой учительницы физики Елены Николаевны Боковой, которая была едва старше своих учеников. Конечно, в понимании физики Андрей превосходил свою неопытную учительницу. И постоянно (к всеобщему удовольствию товарищей и к неописуемому огорчению учительницы) проделывал такой «аттракцион». Он поднимался и сообщал, что придумал вечный двигатель. (В школе царил дух свободы, и не дать гимназисту высказаться считалось недопустимым). Он выходил к доске и описывал свой «прибор», как правило, весьма хитроумный, и найти «ошибку» было очень затруднительно. Учительница что-то пробовала возражать, но её аргументы легко разбивались. Время шло, ученик были в восторге, а учительница чуть не плакала, проклиная, должно быть, тот час, когда связала свою жизнь со школой.
Прошли годы, десятилетия… Бывшие ученики собирались у своей любимой, некогда молодой, а теперь уже постаревшей учительницы 3 июня, в день её именин. Они приходили к ней в течение почти 60 лет, и она хранила их в своем сердце и не давала умереть памяти в них самих. Имя Андрея Николаевича произносилось там с благоговением, а старая учительница всегда с улыбкой рассказывала о переживаниях своей молодости, в которых он были «виновником».
В своем письме своему другу П. С. Александрову (от 17 мая 1943 года) А. Н. Колмогоров описывает некоторые параллели и воспоминания, которые на него нахлынули после чтения любимой им новеллы Томаса Манна «Тонио Крюгер» и, пришедших ему в голову, сопоставлений героев новеллы со своими одноклассниками.
«В 1914-1916 годах Кристя Кроткова, Валя Бочаров и я образовывали триумвират, господствующий всецело в классе (в нем тогда ещё было 16-18 учеников). Мы получали всегда круглые «вполне успевает» (большего, как я рассказывал, у Евгении Николаевны не полагалось: были три отметки: «успевает», «вполне успевает», «не успевает»), однако никогда не отказывались подсказывать неуспевающим и были одновременно первыми учениками и зачинщиками всех шалостей. А когда Евгения Альбертовна… затеяла «Общество друзей хорошего поведения» со взаимным наблюдением и жетончиками, которые товарищи сами должны были отнимать у про-винившихся, то мы организовали целый бунт – на нем затея и провалилась….
Триумвират распался в 1916-1917 году с появлением в классе Бори Попова и Коли Селиверстова. Боря Попов в последствии сделался толстовцем… Но тогда он был представителем партии уличных драчунов с допущением нечестных ударов, неприличных анекдотов, и т.п. В части анекдотов его поддерживал и Миша Шмелькин. Над этими «противниками» сначала триумвират одержал полную победу: за воротами гимназии они были остановлены, Валя Бочаров отошел в сторону, я вздул Борю Попова, а Кристя – Мишу Шмелькина (это для примазавшегося к партии уличных мальчишек было уже полным уничтожением).
Распадение триумвирата, тем не менее, произошло незаметно…
Я же все более дружил с Колей Селиверстовым по ученой линии, а по линии шалостей – парадоксальным образом вошел в новый триумвират из Коли Селиверстова, Бори Попова и меня, сидевших на задней парте и смущавших учителей тем, что двое из нас (я и Коля), ничего не слушая на уроках и занимаясь под партой своими приватными делами, тем не менее, превосходили девиц, сидевших на первой парте…
Весь период 1914 – 1917 года вмещал, впрочем, ещё:
1) Разыскания по энциклопедии Брокгауза о пантеизме, манихействе, Франциске Ассизском и т.п. и соответствующие молитвенные и экстатические состояния (весна 1915).
2) Увлечение стихами Соловьева и Гамсуна (я пробовал тогда читать «Пана», особенно по поводу пантеизма, но, кроме описаний природы, там ничего не воспринял»).
3) Первое увлечение наукой при чтении «Жизни растений» Тимирязева (осень 1915). Более раннее увлечение арифметическими задачами не рассматривались субъективно как увлечение «наукой», а просто как род спорта.
4) Увлечение историей с Колей Селиверстовым (1916-1917)».
Более всего привлекала учащихся атмосфера творчества, царившая в гимназии. Андрей Николаевич вспоминал (цитируется по книге [4]): «В гимназии классы были маленькие (15-20 учеников). Значительная часть учителей сама увлекалась наукой. Иногда это были преподаватели университета, наша преподавательница географии сама участвовала в интересных экспедициях. Многие школьники состязались между собой в самостоятельном изучении дополнительного материала, иногда даже с коварными целями посрамить своими знаниями менее опытных учителей. Делался опыт ввести в традицию публичную защиту кончающими учащимися выпускного сочинения (типа вузовской дипломной работы). По математике я был одним из первых в своем классе, но первыми более серьезными научными увлечениями в школьное время для меня были сначала биология, а потом русская история…
В детские годы мечты о будущей деятельности законно переплетаются с игрой. В 11-12 лет я затратил немало труда на собирание подробных сведений о необитаемых островах южных океанов, так как собирался навербовать выходцев из разных стран и организовать на этих островах некое идеальное государство, для которого мною даже была написана конституция. Был предусмотрен и военный флот для защиты от возможных посягательств на нашу свободу.
Но в 13-14 лет такие занятия были уже дурашливостью. К тому же наступил 1917 год, и мы все, товарищи по школе, вдруг стали взрослыми.
Первым серьезным планом дальнейшей жизни и работы было намерение заняться лесным хозяйством – стать лесничим, сажать леса, растить их и охранять. Увлекала, конечно, и романтика жизни в лесу.
Мои способности к математике к этому времени уже в значительной мере проявились Я решал трудные задачи, а в теории ушел много дальше школьных программ. Высшую математику изучал по статьям в энциклопедическом словаре Брокгауза и Эфрона, что не слишком легко, так как статьи эти имели не учебный характер, а, скорее, справочный.
Но оформленная мысль стать математиком, исследователем, самому делать в математике серьезные открытия, продвигать математическую науку вперед, пришла не сразу. Скорее всего, в шестнадцать лет …
Общей установкой на поиски для себя серьёзного, нужного дела я обязан семейной традиции (особенно воспитавшей меня В.Я Колмогоровой) и атмосфере, господствовавшей в замечательной частной гимназии Е.А. Репман, в которой я учился. Научные увлечения шли от учителей этой гимназии, но культивировались особенно азартно в кружке друзей, из которых назову братьев Селиверстовых (Глеб – математик, Николай – историк)…
В 1918-1920 годах жизнь в Москве было нелегкой. В школах серьезно занимались только самые настойчивые. В это время мне вместе со старшими пришлось уехать на постройку железной дороги Казань – Екатеринбург. Одновременно с работой я продолжал заниматься самостоятельно, готовясь сдать экстерном за среднюю школу. По возвращении в Москву я испытал некоторое разочарование: удостоверение об окончании школы мне выдали, даже не потрудившись проэкзаменовать».
- В 1920 году Андрей Николаевич поступил одновременно на физико-математический факультет Московского государственного университета имени М. В. Ломоносова, на математическое отделение Химико-технологического института имени Д. И. Менделеева и оформился вольнослушателем на историческом факультете университета. На историческом факультете, будучи первокурсником, на одном из исследовательских семинаров он со значительным успехом выступает с научным докладом, в котором речь шла об анализе земельных отношений в Новгороде, а при его подготовке им «использовались … некоторые приемы математической теории». Этот многостраничный доклад, уже после смерти А.Н. Колмогорова, был опубликован в виде отдельной книги и получил высокую оценку уже современных специалистов-историков. Поступление в Химико-технологический институт А.Н. Колмогоров сам объяснял так: «Не бросал мысль о технической карьере, почему-то меня увлекала металлургия», «Техника тогда воспринималась как что-то более серьезное и необходимое, чем чистая наука». Первые увлечения прошли, перевесил интерес к математике и Андрей Николаевич начал её активно изучать и, уже с первых курсов, начинает свои собственные научные исследования.
В статье «Как я стал математиком» (см. [4]) пишет: «Сдав в первые же месяцы экзамены за первый курс, я, как студент второго курса, получил право на 16 килограммов хлеба и 1 килограмм масла в месяц, что, по представлениям того времени, обозначало уже полное материальное благополучие. Одежда у меня была, а туфли на деревянной подошве я изготовил себе сам…
Впрочем, в 1922-25 годах потребность в дополнительном заработке, к весьма маловесной в то время стипендии, привела меня в среднюю школу. Работу в Потылихинской опытно-показательной школе Наркомпроса РСФСР я вспоминаю теперь с большим удовольствием. Я преподавал математику и физику (тогда не боялись поручать преподавание двух предметов сразу девятнадцатилетним учителям) и принимал самое активное участие во всей жизни школы (был секретарем школьного совета и воспитателем в интернате».
«Работа в Потылихинской школе оказала очень большое влияние на всю последующую жизнь Андрея Николаевича – пишет В. М. Тихомиров в [1]. … Ему было 19 лет, когда он начал преподавание, но ему сразу удалось завоевать признание и доверие своих школьников (в основном, детей фабричных рабочих) силой своего интеллекта. Он преподавал два труднейших предмета… и еще руководил кружком юных биологов. Андрей Николаевич рассказывал, что большое впечатление на своих школьников он произвел, принеся в школу номера “Comptes Rendus” и “Fundamenta Mathematicae” с напечатанными там своими статьями на иностранном языке.
Однако именно в Потылихинской школе Андрею Николаевичу пришлось испытать и очень большое огорчение. «В школьные годы я был довольно болезненным ребенком. На школьном дворе во время игр падал в обморок. Потылихинская школа, между прочим, оказала на меня в этом отношении некоторое действие. Молодому учителю очень хотелось быть популярным. Для этого мне не хватало именно физических возможностей. В те времена каждый класс школьников выбирал себе классного руководителя – такой был порядок в школе. И был у меня любимый класс, про который я был совершенно уверен, что именно меня они выберут своим классным руководителем. И вдруг ко мне приходят и говорят, что они выбрали физкультурника! Потом педагогический совет им разъяснил, что физкультурник все-таки по положению не может быть классным руководителем. Тогда они второй раз собрались и выбрали меня. А на меня это произвело чрезвычайное впечатление и содействовало тому, что я постарался исправиться, побольше ходить на лыжах, плавать научился как следует и т.д. В 1924 году Андрей Николаевич организует свой первый поход со школьниками — в Крым, и стой поры походы становятся важной частью его жизни».
В студенческие и аспирантские годы А.Н. Колмогоров опубликовал 18 математических работ! Это, видимо, непревзойденный до настоящего времени результат эффективности обучения на механико-математическом факультете МГУ имени М.В. Ломоносова. Своими научными руководителями и наставниками Андрей Николаевич считал П.С. Урысона, П.С. Александрова, В.В. Степанова, А.К. Власова, а главным своим учителем – Николая Николаевича Лузина.
Школа Лузина («Лузитания»), составившая ядро математической школы Московского университета — особое явление и её феномен поражает. Мы не в состоянии здесь описать подробно этот феномен, но важно иметь хотя бы представление о той возвышенной атмосфере творчества и взаимоотношений, которая царила в «Лузитании». Один из первых учеников Н.Н. Лузина, создатель впоследствии собственной топологической школы, академик Александров П.С. в одной из своих статей пишет: «Я впервые встретился с ним будучи студентом 2-го курса. Впечатление от этой встречи было, можно прямо это сказать, потрясающим, и я запомнил его на всю жизнь. Обратившись к нему после лекции за советом, как мне заниматься математикой дальше, я был прежде всего поражен внимательностью и – не могу найти другого слова – уважением к собеседнику — как не странно звучит этот слово, когда речь идет о беседе уже знаменитого, хотя и молодого ещё, ученого с 18-летним студентом. Выслушав меня, Лузин посредством умело поставленных вопросов очень скоро разобрался в характере моих математических склонностей и сразу же доступной мне форме обрисовал основные направления, которые он мог мне предложить для дальнейших занятий; очень осторожно он сам меня склонил к выбору одного из этих направлений, причем все это было сделано тонко, без всякого нажима и – как я теперь могу сказать – правильно».
Лузин ввел совершенно новые методы работы с молодежью, ставя перед совсем молодыми людьми сложные задачи, которые были пока не доступны другим математикам мира. Но главное, это постоянное общение как во время работы семинаров (с докладами результатов собственных исследований участников), так и между заседаниями семинаров. Часто встречи проходили на квартире у Н.Н. Лузина (куда приходили члены «Лузитании» по специальному расписанию в количестве 1-3 человек), где также устраивались и коллективные встречи. Он объединил своих учеников в замечательный, работоспособный и неповторимый коллектив. П.С. Александров писал, что «Никогда не забуду тех насыщенных самой живой математикой разговоров, которые тогда происходили. Эти разговоры иногда затягивались за полночь, но когда бы они не кончались, за ними следовал чай с неизменным ореховым тортом. За этим чаем – уже не в кабинете, а в столовой квартиры Лузиных – разговоры принимал другой, нема-тематический характер и касались раз-личных вопросов культурной жизни». А.Н. Колмогоров в своих размышлениях на тему общих вопросов развития математики отмечал: «Математика в её историческом аспекте состоит не только из теорем, а из совместного биения сердец, имевшего место в Лузитании».
Во время обучения в университете А.Н. Колмогоров не только получил первоклассное образование и стал известным всему миру математиком, но и получил также опыт преподавания в школе, был участником правильно и ясно устроенных взаимоотношений между научными руководителями и начинающими исследователями. Полученный положительный опыт такого общения с молодыми людьми сыграл значительную роль во всей его деятельности как ученого и преподавателя.
- В 1929 году А.Н. Колмогоров был принят на работу в институт математики и механики при МГУ, а в 1931 году стал профессором МГУ и эти свои профессорские обязанности он выполнял до конца своей жизни. Интересно, что в 1929-1931 годы, будучи научным сотрудником МГУ, по совместительству он заведовал кафедрой математики в Индустриально-педагогическом университете им. К. Либкнехта (который вошел в состав МГПИ имени В.И. Ленина).
А.Н. Колмогоров П.С. Александров
Педагогические раздумья и забота о постановке математического образования в массовой школе нашли свое отражение в вышедшем в свет в 1939 году учебнике «П.С. Александров, А.Н. Колмогоров, Алгебра. Пособие для средних школ. Часть Первая. – М.: Учпедгиз, 1939». В аннотации издательства к этой книге говорится: «Предлагаемый вниманию читателей учебник алгебры П.С. Александрова и А.Н. Колмогорова вы-пускается в 1939 году пробным изданием для ознакомления с ним широких кругов преподавателей математики и научных работников… При оставлении отзывов и замечаний необходимо иметь в виду, что настоящий учебник подготавливается издательством для замены действующего ныне стабильного учебника алгебры Киселева». Авторы учебника в своем предисловии пишут, что «Мы везде стремились соединить понятность изложения с его достаточной обстоятельностью и логической безупречностью. При этом мы исходили из убеждения, что наша книга будет верным и надежным руководителем для учащегося не только при первом знакомстве с предметом, но и при дальнейшем изучении математики». Из этого текста видно, что книга написана в том числе и для тех, кто проявляет интерес к более глубокому изучению математики. Работе с такими школьниками в будущем А.Н. Колмогоров посвятит более 30 лет своей жизни.
В Колмогоровской школе при МГУ и у автора настоящих строк сохранились два экземпляра этого учебника «Алгебра». На одной из них имеется дарственная надпись А. П. Киселеву, но эту книгу адресат не получил, ввиду своей болезни и скорой смерти. Второй экземпляр – это рабочий экземпляр авторов учебника, в котором к страницам учебника приклеены дополнительные листочки, на которых рукой П. С. Александрова выписаны все критические замечания читателей книги — это выдержки из «Учительской газеты», журнала «Математика в школе», протокола совещания учителей от 8.Х.40 и из писем отдельных учителей и математиков Самарканда, Одессы, Красноярска, Чернигова, Владимира и др. городов страны, а также от авторов действующих тогда учебников А.П. Киселева и А.Н. Барсукова. Какой ответственный подход к важнейшему для страны делу, как у авторов, так и у издателей!
Вторая часть задуманного учебника «Алгебра. Часть Вторая» так и не появилась в печати, помешала война и последующие за Победой годы восстановления страны от всеобщей разрухи. Но о тщательной продуманности этой второй части учебника отчетливо свидетельствуют, в частности, три статьи авторов: одна — в «Учительской газете» и две — журнале «Математика в школе» 1940 года. Все эти работы посвящены именно второй части учебника (неравенства, действительные числа, скалярные величины и др.)
Ещё одно свидетельство тщательности и добросовестности отношению к проблемам образования в школе обнаруживается в книге Н. Н. Никитина «Начальный курс геометрии для семилетней школы. Учебный материал для YI класса» (М.: Издательство АПН РСФСР, 1952) с дарственной надписью, адресованной П.С. Александрову. На обложке книги указано, что книга представляет собой «Учебный материал для опытной проверки», выпущена тиражом 3000 экземпляров, а на последней странице обложки типографским шрифтом указано «Бесплатно». Внутри этой небольшой книги имеется около десятка мест с замечаниями П.С. Александрова и автор настоящей статьи уверен в том, что все эти замечания обсуждались с А.Н. Колмогоровым, так как сам экземпляр этого пробного учебника сохранился в ФМШ при МГУ в его рабочем кабинете.
В дневнике А.Н. Колмогорова в [5] имеется любопытная запись от 1 декабря 1943 года, оформленная в виде таблицы, содержащая календарный план того «как сделаться великим человеком, если на это хватит охоты и усердия». В нем присутствуют, наравне с чисто научными и организационными делами, и такие позиции:
1944-1953 Алгебра и элементы анализа для средней школы.
1954-1963 Геометрия и тригонометрия для средней школы.
1964-1973 Логика для средней школы.
Тем самым, мы видим, что планы А.Н. Колмогорова о его личном участии в деле совершенствования школьного математического образования были долгосрочны, обширны и нацелены на дальнюю перспективу. Все эти планы были реализованы (правда, не в указанные в дневнике сроки). Современные школьники учатся по учебнику «Алгебра и начала анализа», куда вошла и тригонометрия.
Долгое время, в школе использовались учебники по геометрии, написанные им в соавторстве с другими педагогами или подготовленные под его редакцией. Эти геометрические учебники сейчас уже не действуют в качестве стабильных, но многое из того, что в них содержится до сих пор используется лучшими педагогами страны. Как руководитель авторского коллектива А.Н. Колмогоров не только организовывал его работу, но определял всю структуру текста, изучал разные варианты изложения, разрабатывал и печатал материалы, собственноручно готовил эскизы чертежей и пр., а потом редактировал и снова дополнял, изменял. О многочисленных трудностях с написанием этих учебников имеются прекрасные статьи А.М. Абрамова и Р.С. Черкасова – соавторов А.Н. Колмогорова (см.[2]). Очень жаль, что эти учебники по геометрии были отторгнуты и не получили нужной поддержки не только в официальных кругах, но и у многих «братьев по математическому цеху».
В стенах ФМШ при МГУ был апробирован вводный курс математической логики, часть которого вошла в первый выпуск учебника для физико-математических школ, а на первом курсе механико-математического факультета МГУ появился обязательный курс логики для первокурсников.
О целесообразности введения элементов математического анализа в школьный курс А.Н. Колмогоров (вместе со многими другими учеными) многократно высказывался и постоянно отстаивал свою точку зрения: «Вряд ли нужно доказывать, насколько желательно с общеобразовательной точки зрения достигнуть того, чтобы все учащиеся могли вполне конкретно понять хотя бы ньютоновскую концепцию математического естествознания». Он считал, что курс анализа в школе должен быть не очень формальным и наглядным. Имея в виду свою работу учителем в Потылихинской школе и в школе при МГУ, он подчеркивал, что: «Опыт наглядного преподавания начал анализа говорит, что эти начала могут быть изложены в форме, в которой они совсем не воспринимаются как что-либо более трудное, чем обычный, чисто алгебраический материал». После многочисленных вариантов изложения этого курса, обсуждений в педагогической печати, экспериментов в многочисленных школах страны сейчас учебник для него с успехом «работает» в массовой школе. Кроме того, реформаторские идеи А.Н. Колмогорова и их реализации стали конкретным примером и сейчас имеется много других учебников по этому курсу, написанных с участием известных ученых и преподавателей.

 Среди автографов А.Н. Колмогорова сохранился экземпляр учебного пособия «Алгебра и начала анализа», изданного в 1975 году издательством «Просвещение», написанный в соавторстве Б.В. Вейцем, И.Т. Демидовым, О.С. Ивашевым-Мусатовым, С.И. Шварцбурдом. Этот экземпляр книги выглядит «очень пухлым» от большого количества листочков с записями А.Н. Колмогорова, на которых имеются конкретные замечания по тексту, критика списка задач и решения отдельных из них, указания на явные неточности и ошибки, замечания на свободных полях страниц, знаки вопросов и пр.
Среди автографов А.Н. Колмогорова сохранился экземпляр учебного пособия «Алгебра и начала анализа», изданного в 1975 году издательством «Просвещение», написанный в соавторстве Б.В. Вейцем, И.Т. Демидовым, О.С. Ивашевым-Мусатовым, С.И. Шварцбурдом. Этот экземпляр книги выглядит «очень пухлым» от большого количества листочков с записями А.Н. Колмогорова, на которых имеются конкретные замечания по тексту, критика списка задач и решения отдельных из них, указания на явные неточности и ошибки, замечания на свободных полях страниц, знаки вопросов и пр.
- В декабре 1963 года по инициативе видных ученых И. К. Кикоина, А. Н. Колмогорова при поддержке И. Г. Петровского, М. В. Келдыша и др. была открыта специализированная физико-математическая школа при Московском государственном университете имени М. В. Ломоносова; см. [6]. Всего таких школ при ведущих университетах страны была открыто четыре – ещё при Новосибирском (которая начала работу раньше Московской), Ленинградском и Киевском университетах.
Эти школы задумывались как школы научного творчества, отличались от других школ, как по содержанию программ, так и методам работы в них. Школа при МГУ с самого момента её открытия называлась Колмогоровской школой, что уважительно фиксировало и подчеркивало личность её научного руководителя. Сейчас, в канун своего 50-летия, эта школа официально называется «Школой имени А.Н. Колмогорова», которая входит в состав Специализированного учебно-научного центра МГУ имени М.В. Ломоносова. Более двадцати лет своей жизни А.Н. Колмогоров отдал этой школе, которую сам создал, вдохнул в неё жизнь, читал в ней лекции, вел семинарские занятия, руководил работой кружков для школьников и методическим объединением преподавателей математики, работал в летних школах для поступающих, возглавлял попечительский совет, устраивал музыкальные и литературные вечера, ходил с детьми и преподавателями в туристические походы, рассказывал о своих путешествиях и делал многое, многое другое. Описать всю его огромную работу в школе при МГУ в этой статье невозможно (подробно см. [7,8]) и мы ограничимся только некоторыми перечислениями и небольшими замечаниями. Отметим также, что формируя методическую систему преподавания, формы и методы работы с преподавателями и учениками, А.Н. Колмогоров использовал свой личный опыт домашнего обучения, учебы в гимназии Репман и работы учителем в Потылихинской школе.
Школы при университетах, как уже отмечалось, задумывались как школы научного творчества, причем не только в области математики: «Существенно, что здесь в интернате, школьники приходят в соприкосновение с творческой мыслью. Это наш запрос, но по всем предметам! Метод работы – имитация научного исследования, шаг за шагом находить, вычислять нечто…, а не давать готовенькое». Среди основных целей преподавания математики и обучению ей школьников и поныне входят такие как воспитание научного мировоззрения, подготовка к обучению в университете и приобретение навыков творческой деятельности.
Для реализации таких целей обучения в школу, естественно, приглашались (и приглашаются сейчас) преподаватели из МГУ, обладающие не только опытом педагогической деятельности, но и опытом научной работы, в частности, в различных областях математики.
В школе принята лекционно-семинарская система преподавания, но лекции по математическим курсам длятся один академический час. Курсы лекций А.Н. Колмогорова отличались значительной глубиной, в них часто речь шла о «настоящей» математике и они всегда были нацелены на приобщение к исследовательской и творческой работе. Так, например, описывая свой вводный курс математического анализа А.Н. Колмогоров писал: «Лекционный курс начинается с общего понятия отображения (функции) и развивается с одной стороны в направлении изучения геометрических преобразований и кинематики, а с другой стороны в виде наглядного введения в анализ… с первыми примерами дифференциальных уравнений». Курс геометрии, который дважды читал А.Н. Колмогоров в школе начинался с аксиоматики аффинной плоскости (и затеи и пространства), с тщательным анализом на независимость, непротиворечивость, полноту. Здесь появлялись конечные и недезарговы плоскости, преобразования плоскости и их классификация и пр. Усвоение этого курса требовало от учеников и преподавателей значительных усилий, но витавший вокруг обучающихся и обучающих дух созидания и творчества, происходящий на их глазах, быть может, давал участникам этого процесса обучения гораздо больше, чем какая-то конкретная «сумма знаний». Понимая трудности усвоения необычного курса, А.Н. Колмогоров сам печатал на машинке конспекты лекций и раздавал их преподавателям (так он делал и для поддержки некоторых разделов курса математического анализа).
Отличительной особенностью школы является (во времена Колмогорова особенно) так называемый математический практикум. При его организации А.Н. Колмогоров писал: «Часы математического практикума, проводящегося, в идеале, для всего потока, используется частично для унификации требования к различным классам письменных контрольных работ, состоящих из серии задач обычного школьного типа. Но в основном эти часы отводятся для выполнения работ большого объема, требующих больших вычислений и чертежного оформления. Например, фактически осуществляется программа оценки числа π, после изучения в классе движения по циклоиде исследуются графически более сложные случаи сложения движений, находятся и изображаются графически решения системы дифференциальных уравнений радиоактивного распада… В проведении практикума участвуют преподаватели, работающие в классах, но отдельная небольшая группа преподавателей его организует и готовит для него материал».
Черновики А.Н. Колмогорова
Другой отличительной особенностью Колмогоровской школы является наличие специальных курсов, специальных семинаров и кружков, которые проводятся преподавателями вне основного учебного времени. Важность этих курсов для учеников можно объяснить тем, что на них не только расширяется математический кругозор, но именно там и возникают постановки новых задач исследовательского характера. Например, в рамках кружка, руководимого А.Н. Колмогоровым, рассматривались различные вопросы дискретной геометрии и, в частности, задача о правильных паркетах (о разбиениях плоскости и сферы на правильные многоугольники).
Сейчас школу имени А.Н. Колмогорова окончило около 10000 учеников, которые практически все становились студентами Московского университета и других первоклассных вузов, добившихся потом больших успехов в науке и ее преподавании, бизнесе, политике и других областях человеческой деятельности. Школа и сейчас пропитана идеями ее создателя как в организации учебно-воспитательного процесса, так и в развитии теории и методики преподавания математики в специализированных классах и школах страны. Отдавая дань Андрею Николаевичу, в школе проходит конкурс решения задач памяти А.Н. Колмогорова, проходят Школьные Колмогоровские чтения, открыт кабинет педагогического творчества, организуются летние олимпиадные школы и летние школы для ее будущих учащихся.
А.Н. Колмогоров, В.В. Вавилов, Д.И. Гордеев в ФМШ
Сейчас уже стало нормой проведение летних математических школ, которые возникли сначала для отбора обучающихся в физико-математические интернаты при университетах. А.Н. Колмогоров был не только инициатором создания таких школ, но сам работал во многих из них: Красновидово 1963-1965, 1968, 1970; Пущино-на-Оке – 1971, 1972, 1975, 1977 и др. Система такой работы со школьниками только расширяется и сейчас является одной из важнейших форм работы с детьми, проявляющих интерес к углубленному изучению той или иной области знаний. Через летние школы проходят сейчас ежегодно тысячи школьников, студентов, будущих и уже состоявшихся преподавателей школ и вузов.
Еще в 1934 году в Ленинграде в нашей стране была организована первая математическая олимпиада школьников и к началу 60-х годов в Москве и Ленинграде сложились прочные традиции в их проведении, которые были заложены группой замечательных математиков и, прежде всего, здесь следует назвать Бориса Николаевича Делоне и Андрея Николаевича Колмогорова. В 1961 году было решено вместе с московской городской олимпиадой устроить и Всероссийскую олимпиаду. Эта идея была реализована благодаря усилиям А.Н. Колмогорова и ректора МГУ – Ивана Георгиевича Петровского. Для организации такой олимпиады была создана постоянно действующая методическая комиссия, которой потом в течение более чем 20 лет бессменно руководил А.Н. Колмогоров. Автор статьи в течение 12 лет был заместителем председателя этой комиссии по математике, и я могу засвидетельствовать, что все основные принципы и фор-мы проведения математических соревнований школьников сегодня сохранились и прочно вошли в практику их проведения. Сейчас вся система организации и проведения предметных олимпиад в нашей стране и во всем мире так сильно разрослась, а сами олимпиады пользуются такой большой популярностью у школьников и их преподавателей, что как-то теперь и нельзя представить себе школьной жизни без олимпиадной деятельности.
Журнал «Квант» был создан в 1969 году и здесь основные усилия по его созданию были предприняты И.К. Кикоиным и А.Н. Колмогоровым. Этот журнал превратился в популярнейшее периодическое издание, рассчитанное на очень активного и заинтересованного читателя. Вообще, вклад Колмогорова в дело популяризации и распространения математических знаний огромен и уникален и его примеру и целеустремленности в этом важнейшем деле организации эффективной работы со школьниками, интересующихся математикой, следуют уже не единицы, а многие тысячи специалистов самых различных направлений. Созданная общими усилиями ученых библиотека, состоящая из научно-популярных книг, постоянно обновляется, а самое главное, ее лучшие образцы востребованы современными читателями и находятся в постоянном использовании.
Мы не в состоянии здесь рассказать о всей титанической работе А.Н. Колмогорова на ниве Просвещения. Более полно обо всем этом рассказано в статье «О педагогическом наследии А.Н. Колмогорова», одного из первых выпускников ФМШ при МГУ, ученика А.Н. Колмогорова, защитившего под его руководством педагогическую диссертацию по проблемам преподавания геометрии А.М. Абрамова (см.[3]).
Академик А.П. Ершов так оценил деятельность А.Н. Колмогорова в деле математического образования: «Не могу не провести параллели с судьбой другого гениального современника Андрея Николаевича Колмогорова – поэта Бориса Леонидовича Пастернака. Та же мера таланта, высокого профессионализма и способности к рядовой работе. Та же несочетаемость со многими реалиями повседневной жизни и обстановки. Та же неразрывная связь с культурой и природой. Та же смертельная ревность и пристрастность со стороны многих собратьев по цеху. То же высокое ощущение своей бескомпромиссной предназначенности для некой человеческой миссии».
В.М. Тихомирову принадлежат такие строки: «Мысли великого человека являются общим достоянием человечества. В них всегда содержатся зерна истины, недоступные для поверхностного анализа. Они должны быть продуманы до конца, детально проанализированы. Так, я уверен, произойдет и с творческим наследием А.Н. Колмогорова, связанным с образованием».
Очень верно заметил В.А. Успенский в своей статье (см. [3]), что если в словах Н.В. Гоголя о Пушкине заменить «поэт» на «ученый», а Пушкин» на «Колмогоров», то мы получим точную характеристику Колмогорова. Вот мысль Н.В. Гоголя: «При имени Пушкина тотчас осеняет мысль о русском национальном поэте… Пушкин есть явление чрезвычайное…».
Литература
- В.М. Тихомиров, Андрей Николаевич Колмогоров. – М.: Наука, 2006.
- Колмогоров в воспоминаниях. Под ред. А.Н. Ширяева. – М.: Физматлит, 1993.
- Явление чрезвычайное. Книга о Колмогорове. Составитель Н.Х. Розов, под общей редакцией В.М. Тихомирова. – М.: ФАЗИС, МИРОС, 1999.
- А.Н. Колмогоров, Математика – наука и профессия. – М.: Наука, 1988.
- Колмогоров. Юбилейное издание в 3-х книгах. Ред.- составитель А.Н. Ширяев. – М.: ФИЗМАТЛИТ,2003.
- КИКОИН. КОЛМОГОРОВ. ФМШ МГУ. Составитель А.М. Абрамов. – М.: ФАЗИС, 2008.
- А.Н. Колмогоров, В.В. Вавилов, И.Т. Тропин, Физико-математическая школа при МГУ, — М.: Знание, 1981 (Новое в жизни, науке, технике. Серия: Математика, кибернетика. №5).
- В.В. Вавилов, Школа математического творчества. – М. РОХОС, 2004.
Д.И. Гордеев, масло В ФМШ при МГУ
Опубликовано в журнале «Потенциал»